1、在纸上写下需要求导的根号表达式
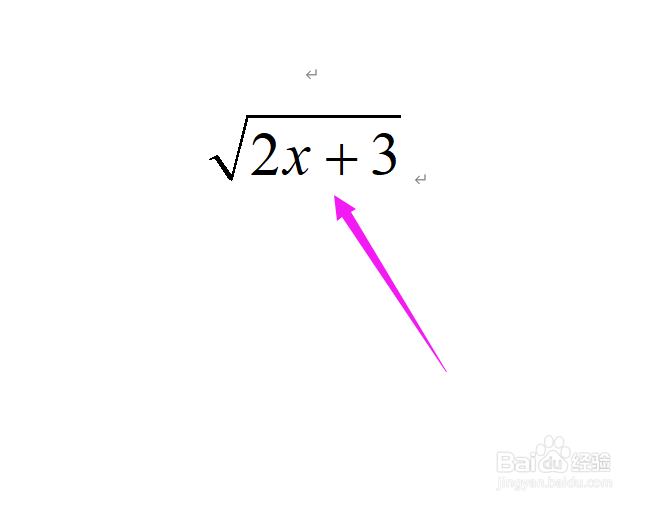
2、将原表达式写成幂函数的形式,即srqt(ax)=(ax)^(1/2)
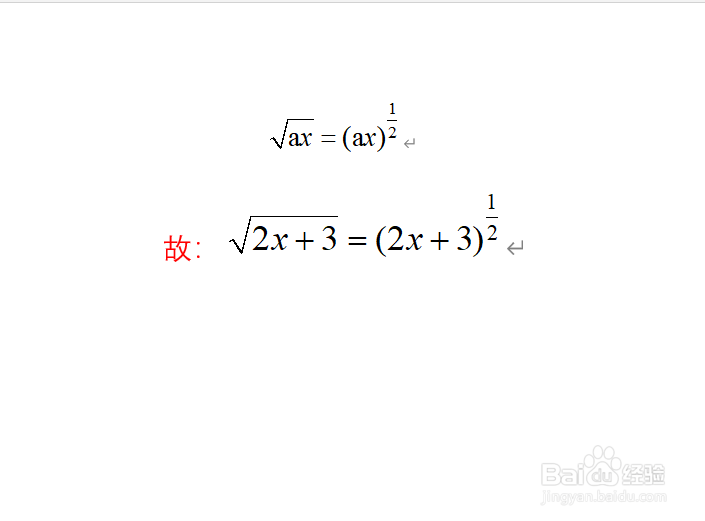
3、利用幂函数的基本求导公式进行求导,即(ax)^b=b(ax)^(b-1)*a
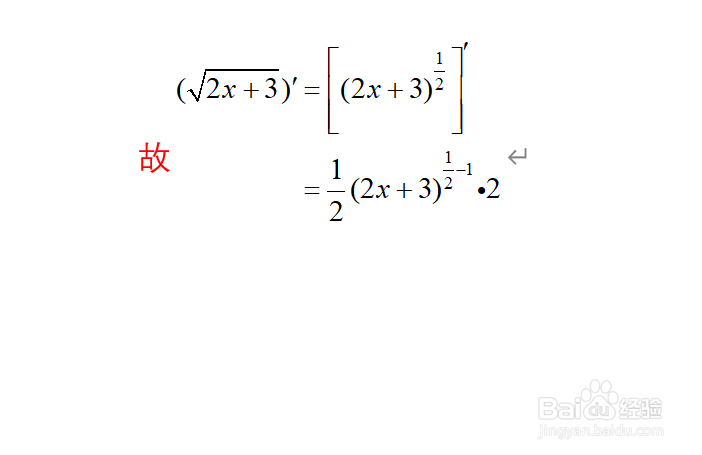
4、代入公式进行化简
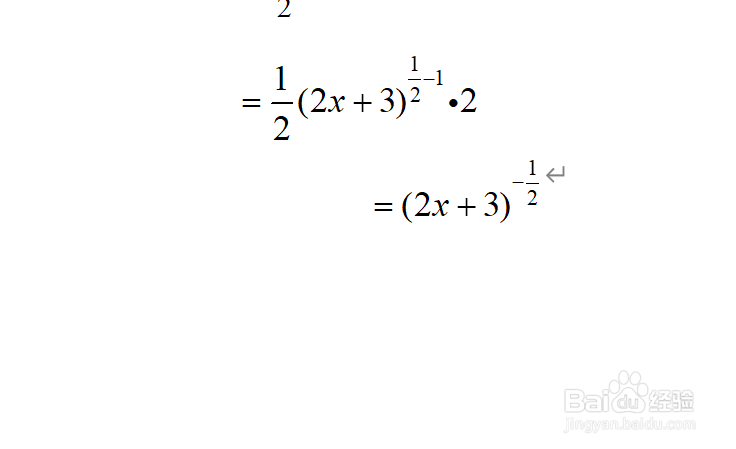
5、将幂函数还原成根号形式,得到最终的求导结果
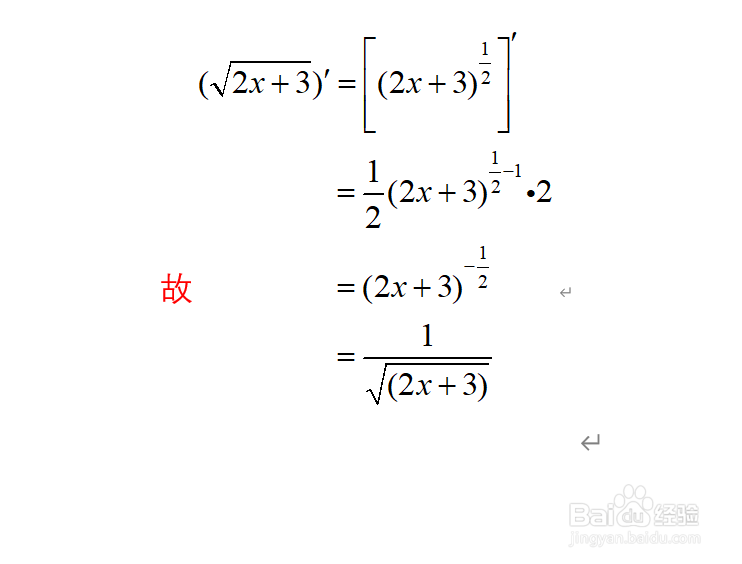
6、总结:1.在纸上写下需要榨施氅汝求导的根号表达式2.将原表达式写成幂函数的形式3.利用幂函数的基本求导公式进行求导,4.代入公式进行化简5.将幂函数还原成根号形式,得到最终的求导结果
1、在纸上写下需要求导的根号表达式
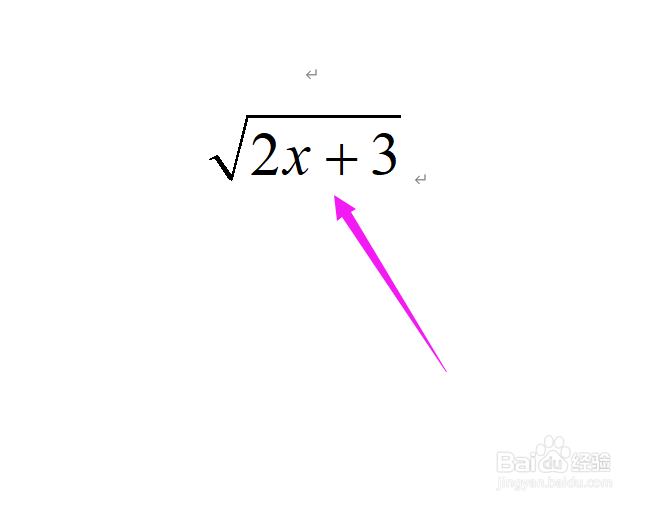
2、将原表达式写成幂函数的形式,即srqt(ax)=(ax)^(1/2)
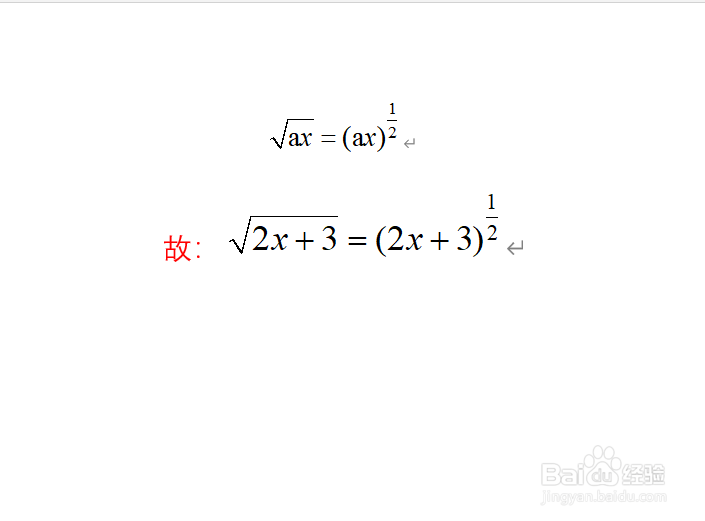
3、利用幂函数的基本求导公式进行求导,即(ax)^b=b(ax)^(b-1)*a
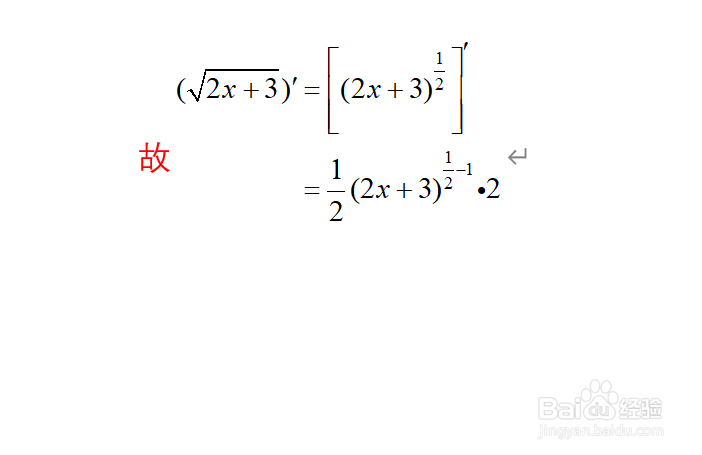
4、代入公式进行化简
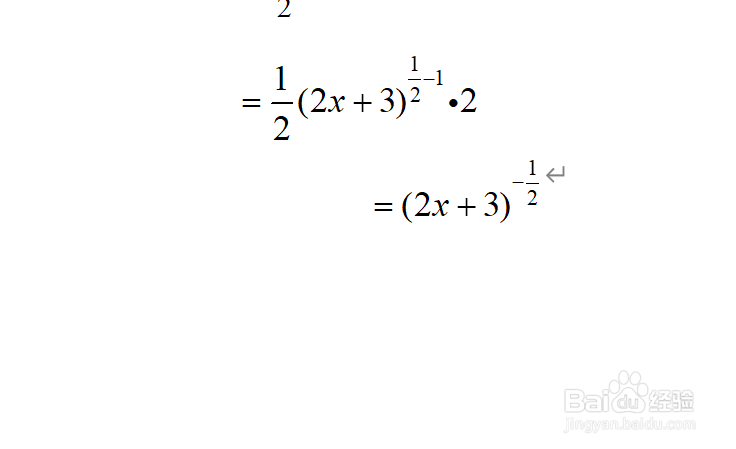
5、将幂函数还原成根号形式,得到最终的求导结果
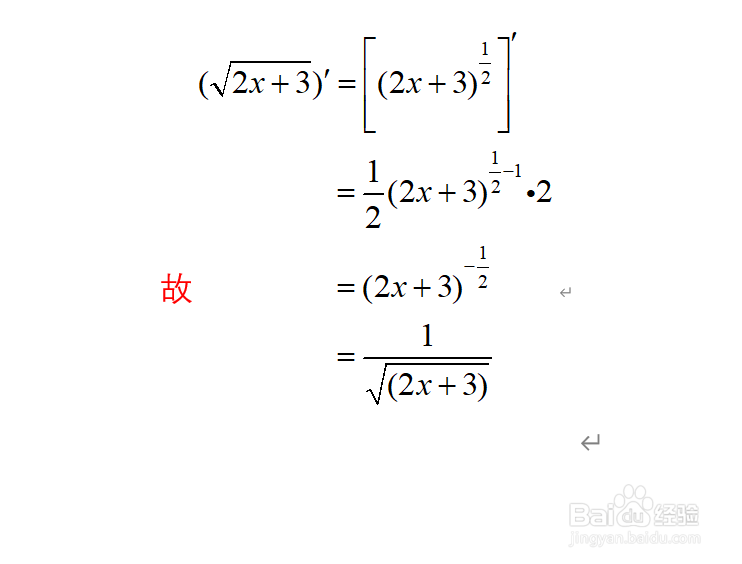
6、总结:1.在纸上写下需要榨施氅汝求导的根号表达式2.将原表达式写成幂函数的形式3.利用幂函数的基本求导公式进行求导,4.代入公式进行化简5.将幂函数还原成根号形式,得到最终的求导结果