傅里叶级数,是用来逼近周期函数的一个方法。把一个周期函数展开成傅里叶级数,有一个好处,那就是处处收敛。因此,只要确保级数在一个周期内能够很好地逼近已知函数,那么这个逼近就可以推广到其它所有的周期里面。


工具/原料
电脑
mma
基本操作
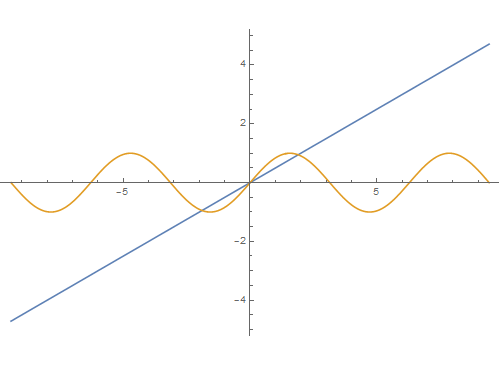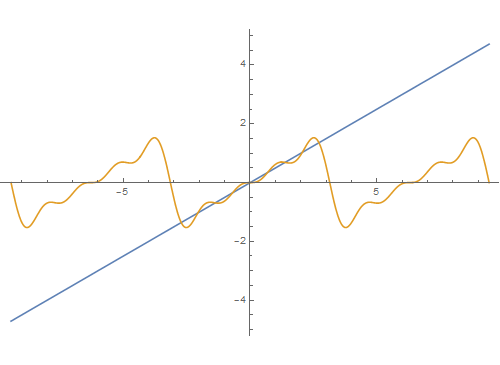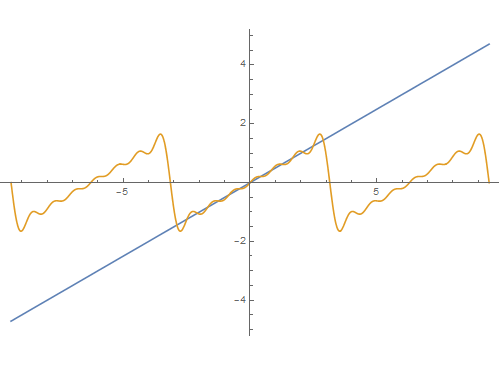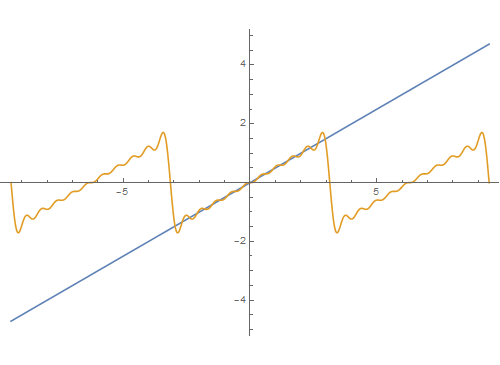
1、先来作一个函数——x/2 的3阶傅里叶级数:FourierSeries[x/2, x, 3】并画出对比图:Plot[{%, x/2}, {x, -3 Pi, 3 Pi}]可以发现,只在区间{-Pi,Pi}上有可比性!
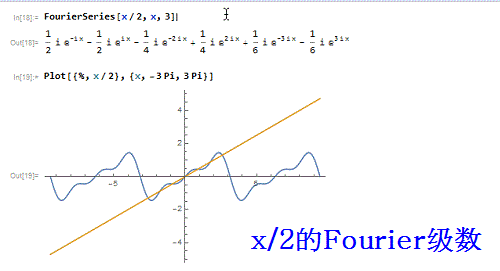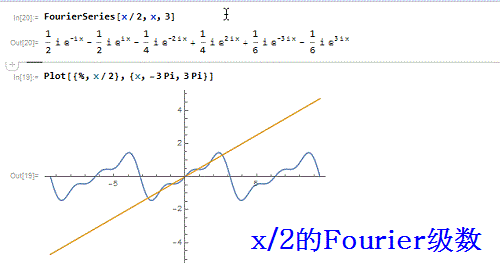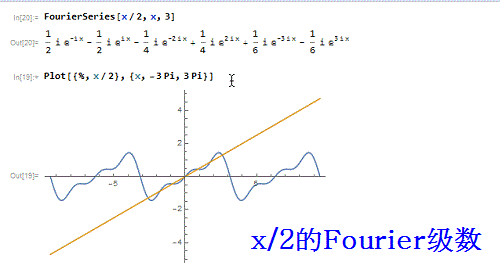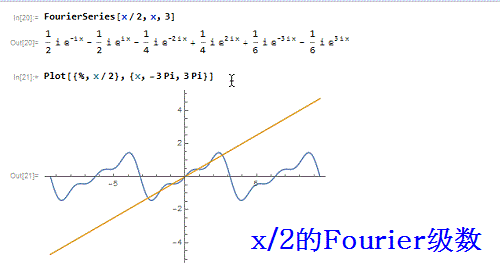
2、把级数的表达式处理一番:FourierSeries[x/2, x, 3] // SimplifyFourierSeries[x/2, x, 3] // Simplify // Traditio荏鱿胫协nalFormFourierSeries[x/2, x, 3] // FullSimplifyFourierSeries[x/2, x, 3] // FullSimplify // TraditionalForm
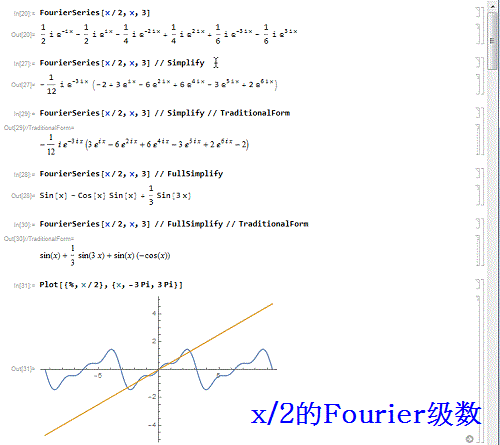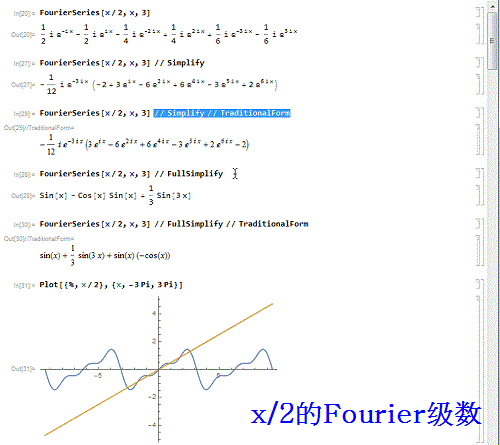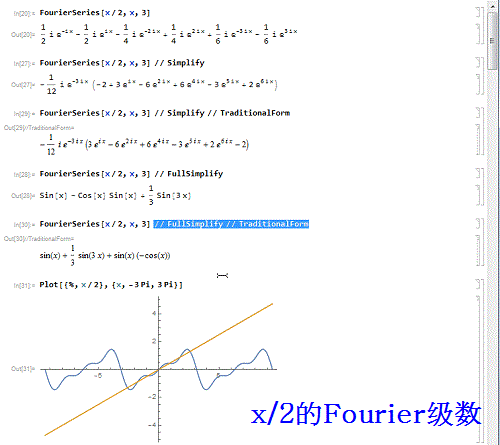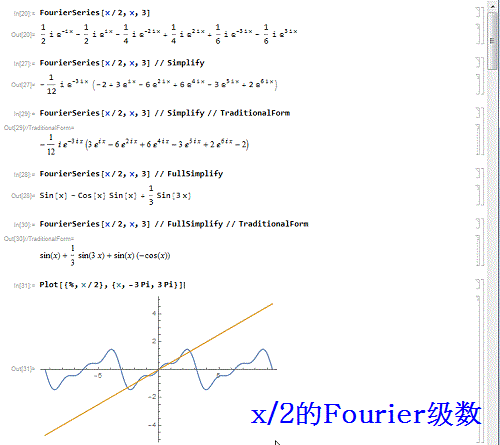
3、用列表的形式,给出t/2的前10阶Fourier级数式:Table[FourierSeries[t/2, t, n], {n, 1, 10}] // FullSimplify // TraditionalForm

4、把列表里的所有表达式画到一起:Plot[%, {t, -3 Pi, 3 Pi}]

5、函数t/2前10阶的Four坡纠课柩ier级数式,对应的逼近程度(互动模拟):Manipulate[Plot[{t/2, E即枢潋雳valuate[FourierSeries[t/2, t, n]]}, {t, -Pi, Pi}, PlotRange -> 2], {n, 1, 10, 1}]
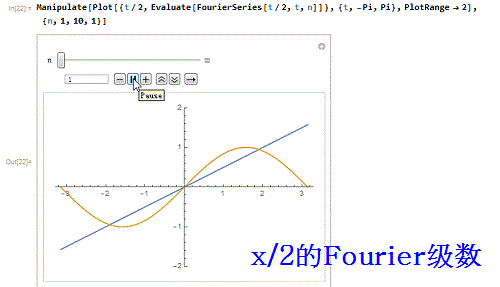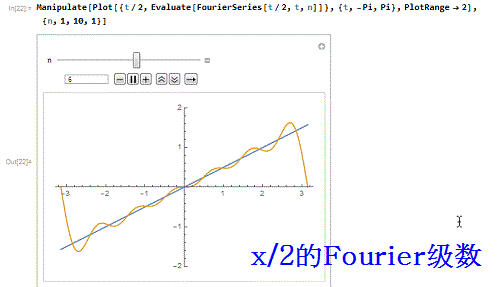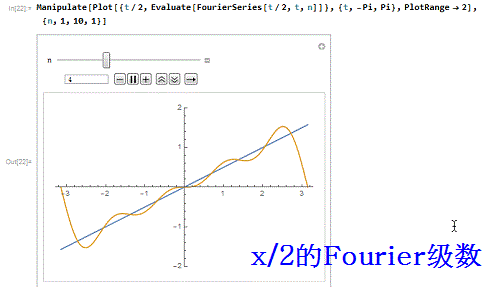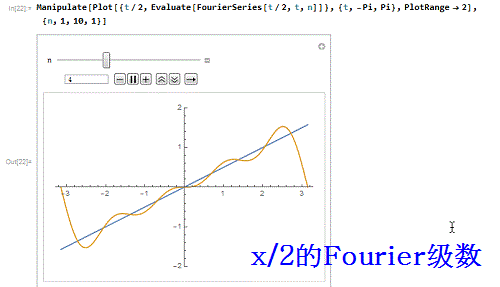

6、Manipulate[Plot[{t/2, Evaluate[FourierSeries[t/2, t, n]]}, {t, -3 Pi, 3 Pi}, PlotRange -> 5], {n, 1, 10, 1}]

7、再尝试一些其它函数,如t^2:Manipulate[Plot[{t^2, Evaluate[FourierSeries[t^2, t, n]]}, {t, -3 Pi, 3 Pi}], {n, 1, 10, 1}]
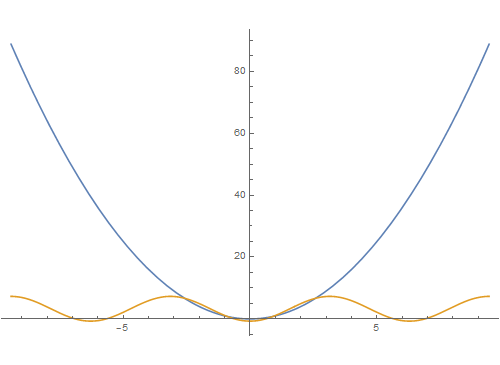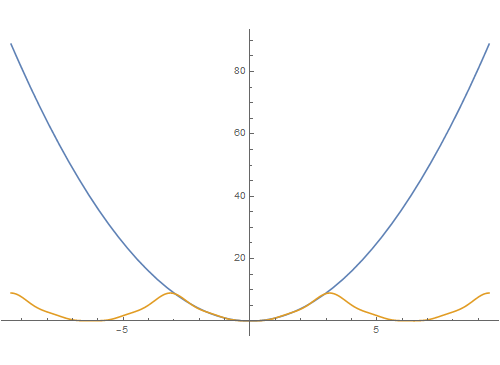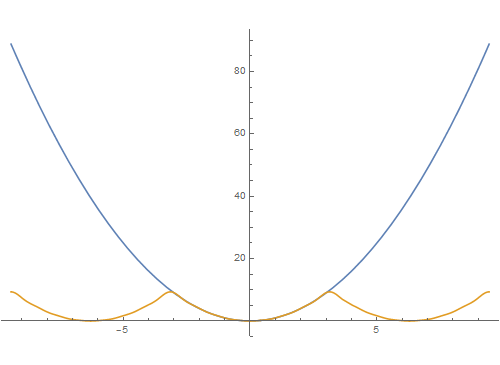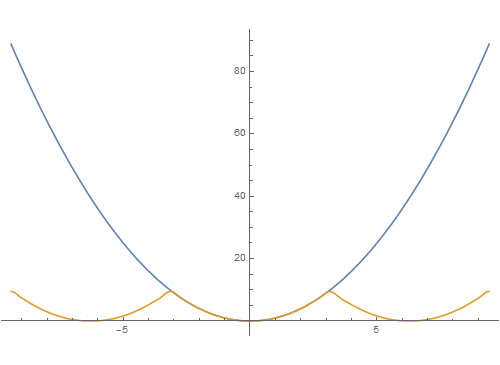
8、一个分段函数:f[x_] = Piecewise[{{1, 0 <= x < Pi}, {-1, -Pi <= x < 0}}];运行互动代码:Manipul锾攒揉敫ate[Show[Plot[f[x], {x, -Pi, Pi}, PlotStyle -> {Thickness[0.01], Red}, PlotRange -> {-1.5, 1.5}], Plot[Evaluate[FourierSeries[f[x], x, n]], {x, -Pi, Pi}, PlotStyle -> {Thickness[0.01], Blue}]], {n, 1, 36, 1}]

9、再来一个分段函数:f[x_] = Piecewise[{{0, 0 <= x < Pi}, {x, -Pi <= x < 0}}]仍旧用上一步的互动代码,逼近情况的互动模拟效果如下!
