力有各种方向,所以我们在研究一种力的时候不能光只会分析横平竖直的力,我们同事应该学会分析其他方向的力,明白他的合成与分解。讲一个不容易分析的力简化成一些简单的力,然后进行计算。
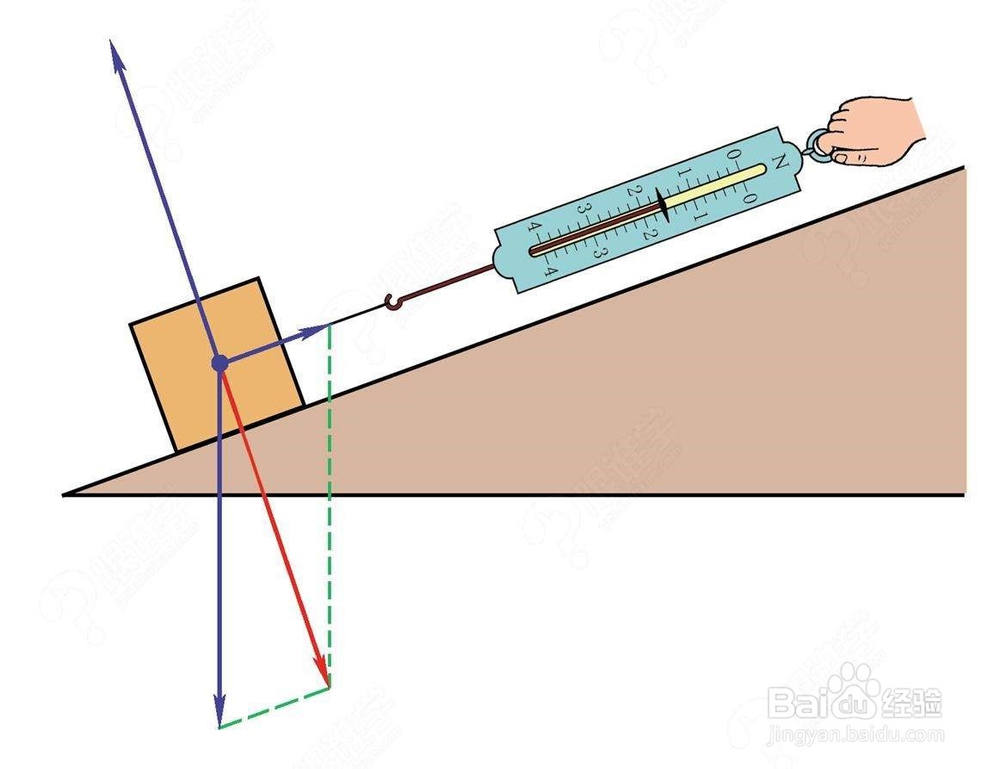

1.力的合成
1、合力与分力:一个力单独产生的效果和几个力共同作用的效果相同,这个力叫做那几个力的合 力,那几个力叫做这个力的分力.

2、力的合成 :求几个力的合力叫做力的合成。

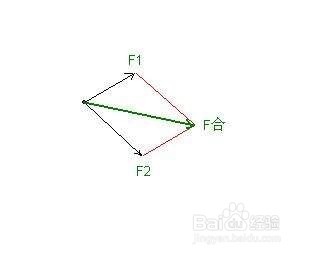
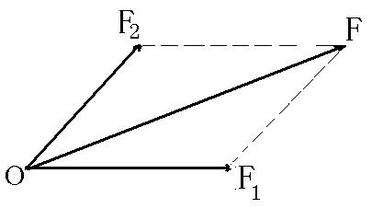
3、矢量运算的法则 :力是矢量,求两个力的左佯抵盗合力时,不能简单地把两个力的大小相加,而应按照平行四边形定则或三角形定则来确定其矢量和。所谓平行四边形定则,即:两个力合成时,以表示这两个力的有向线段为邻边作平行四边形,这两个邻边间的对角线代表合力的大小和方向,这个法则叫做平行四边形定则。所谓三角形定则,即:将需要合成的两个力 首尾相接,从一个力的始端向另一个力的末端引有向线段,该有向线段的大小和方向 就表示合力的大小和方向。

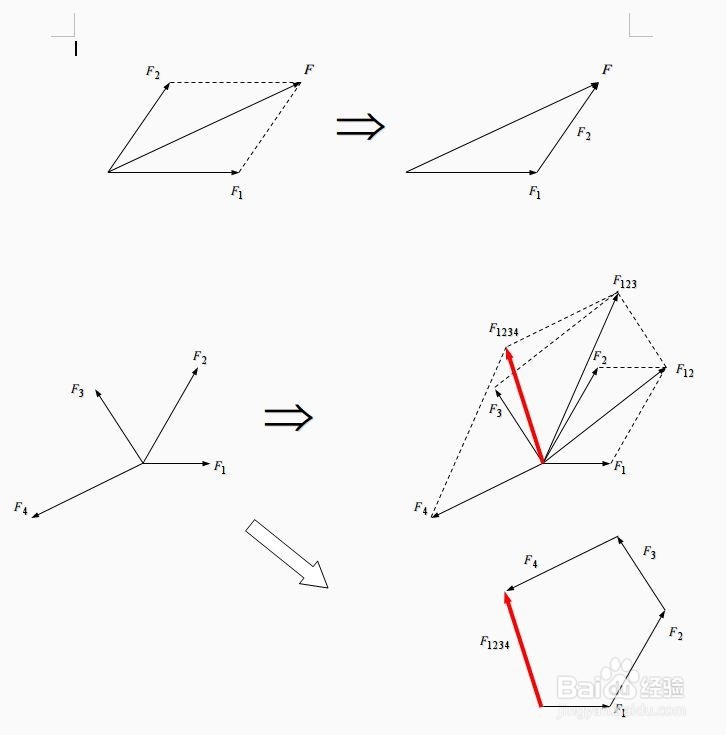
4、共点力:一个物体受到两个或多个力的作用,如果这些力共同作用于一点,或它们的作用 线彗三盛,这些力叫做共点力.

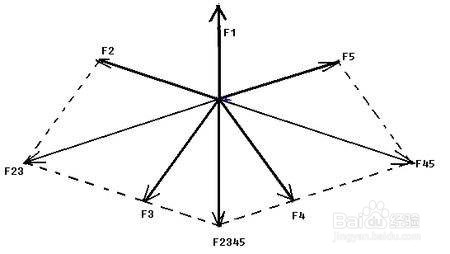
5、合力与分力的关系:两者是等效替代关系。

2.力的分解
1、求一个力的分力叫做力的分解,力的分解同样遵循平行四边形定则.是力的合成 的逆运算。

3.矢量和标量
1、既有大小,又有方向,相加时遵循平行四边形定则或三角形定则的物理量叫做矢量.只有大小,没有方向,求和时遵循算术法则的物理量,叫做标量。
