Mathematica可以很方便的处理一些有趣的数论问题。下面,我们一起来看两个例子——相亲数和半相亲数。

工具/原料
电脑
Mathematica
相亲数(链)
1、给定某个正整数n,怎么求出它的所有约数呢?在Mathematica里面,这个有直接的方法——Divisors(约数)。通过具体的例子,可以知道28的约数是{1, 2, 4, 7, 14, 28},366的约数是{1, 2, 3, 6, 61, 122, 183, 366}。习惯上,把除了数字本身的所有约数,称为它的真约数!

2、如果n的所有真约数之和等于n,那么n就是完全数!约数和[xxx_] := Total[Divisors[xxx]] - xxx;我们来检验一下这些数字是不是完全数:6、28、496、8128、泌驾台佐33550336,结果都是肯定的!

3、相亲数问题:如果a的约数和是b,b的约数和是a,那么a和b互为相亲数。可以很容易地验证220和284是一对相亲数!

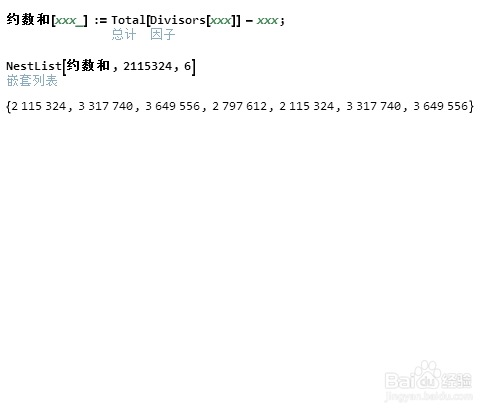
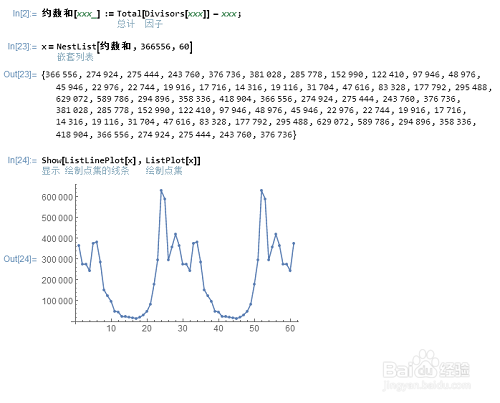
4、更一般的亲和数链:如果存在n个正整数,第一个的约数和等于第二个数,第二个的约数和等于第三个数,……,第n个的约数和等于第一个数;那么,就说这n个数构成一个相亲数链。可以很容易地验证:{2115324,3317740,3649556,2797612}构成一个4阶相亲数链;{12496,14288,15472,14536,14264}构成一个5阶相亲数链;366556可以引出一个28阶相亲数链。

半相亲数
1、定义:设n的所有约数(除了1和n之外)之和,等于m;而m的所有约数(除了1和m之外)之和,等于n。那么,就称m和n是一对半相亲数。半约数和[xxx_] := Total[Divisors[xxx]] - xxx-1;

2、可以验证,48和75是一对半相亲数。

3、不知道是否存在半相亲数链!