正方形的分割问题,是组合几何里面比较有难度的问题。这里面,有很多引人入胜的专题:比如完全正方形、正方形等积三角形分割、正方形分割再拼接、多个正方形分割后再拼接成一个大正方形等问题。
下面简单介绍一下相关内容。

工具/原料
电脑
互联网
正方形分割成等积三角形
正方形能够分割成两个、四个、六个、……、2n个面积相等的三角形,这个过程称为正方形的等积三角形分割。
可以先把正方形沿对角线分成两个面积相等的三角形,再把每一个三角形等积分割为n份;还可以把正方形分割为n个全等的长方形,再沿对角线把每一个正方形分成两份;……;方法实在很多。

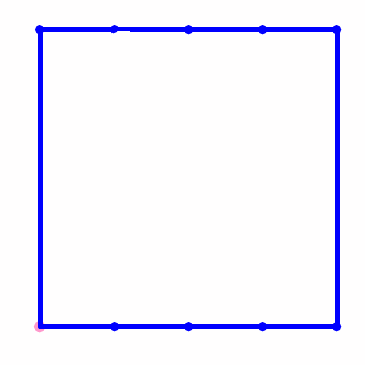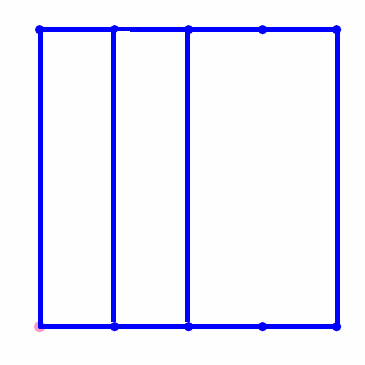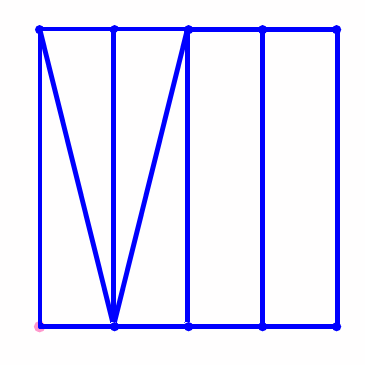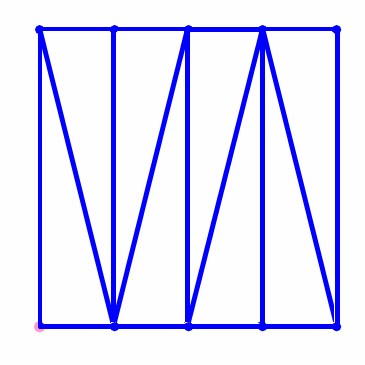
正方形不能分割成奇数个面积相等的三角形。这是一个很难的问题,但相比于完全正方形却又简单得多,至少可以人工证明。
1965年,Richman在《美国数学杂志》上提出猜想——正方形不能分割成奇数个面积相等的三角形。5年后,Paul Monsky证明了这个猜想,因此,相关理论又被称为Monsky理论。

正方形分割再拼接
把正方形分割成五份,再拼接成一个正三角形。其中一个方法是如下:
正方形边长AB=a, AP=r·a(r 等于四次根号3);
PQ//EF交AD于Q;
BE//AP交直线DC于E;
BF⊥AP于F,且B是F、G的中点;
EF交BC于K;
在BE上取点M,使EM=PF;
连结线段GM,并取点N,使MN=PC;
NH⊥GM,交GE于H。
此时,可以证明,△EFG是正三角形,FK=EH,PQ=EK=HG。
事实上,分割成四块,就可以拼出一个正三角形,详见《三角形分割问题举例》。于是,在此基础上,把其中某一份分割成两份,整体上就是五份!
因此,把正方形分割成五份,再拼接成一个正三角形的分割方法是无限多的!
方法一:
这个方法,是由10世纪的阿拉伯数学家Abul Wefa解答的。他的方法是把其中两个正方形各分成四份,第三个正方形不用动!总共是分割成了9份。
具体的步骤不多介绍,如下面的动态图,一看就明白!

方法二:
在GF延长线上截取点D,使得GD=GB;
连结HD交BF于A;
在HG上截取N,使得HN=BA;
作NM//HD交GF于M;
作BE//HD交直线GF于E;
BK⊥HD于K,EZ⊥HD于Z;
三等分线段BE和KZ,产生三个小正方形;
EQ=GM。
可以发现,各部分只要平移就行。这个方法,把小三角形们分割为7份。

方法三:
把三个正方形排到一起,如下图进行分割;
把△ABC平移到△EFD的位置;
把△BEG平移到△CFH的位置,成功。
你数数原来的三个正方形被分割成了多少份!答案是6份,其中仍旧有一个小正方形没动过。

把两个全等的正方形改拼为一个正方形:
给定大正方形ABCD;
作出正方形ABCD各边中点E、F、G、H;
依次连结EF、FG、GH、HE,并取各边中点M、N、P、Q;
连结AM、BN、CP、DQ。
好了,现在能拼出两个正方形了。

五个全等的正方形,分割以后,拼成一个大正方形。
看下图:
给定大正方形ABCD;
作出各边中点E、F、G、H;
依次连结AF、BG、CH、DE;
这四条直线围成正方形 I J K L。
现在,你能拼成五个小正方形吗?

十个全等的正方形组成两个十字形,把一个分割成四份,拼接到另一个上面,组成一个大正方形。
这个问题曾经是中央电视台的一期中学生智力竞赛里面的题目,有趣的是,所有考生都没有做出这个问题,全军覆没!具体原因,大概是时间太紧迫,没有思考的空隙!
具体的步骤如动态图,看了就懂。

注意事项
关于正方形的等积三角形分割问题,只找到少许资料,而且采用了非常抽象的赋值函数进行研究,我目前还看不懂具体的证明过程。
关于正方形的改拼问题,一部分来自互联网,主要的另一部分来自一本书《世界著名平面几何经典著作钩沉几何作图专题卷》,这本书确实不错,是一部不同数学家成果的合集,值得收藏和阅读。
正方形不仅可以改拼成正三角形,而且可以改拼成2个、3个、4个、……、n个正三角形。在上面推荐的书里都可以看到。
正方形不仅可以改拼为正三角形、正五边形,还可以改拼成正六边形、平行四边形、梯形、任意三角形、任意四边形。
正方形可以改拼出任意多个全等的正方形,因为任意矩形、平行四边形都可以改拼成正方形。
我们需要思考的是:改拼的时候,怎么分割,才能使分割的份数最少?
能否用初等数学方法证明:正方形不可能分割为奇数个面积相等的三角形!