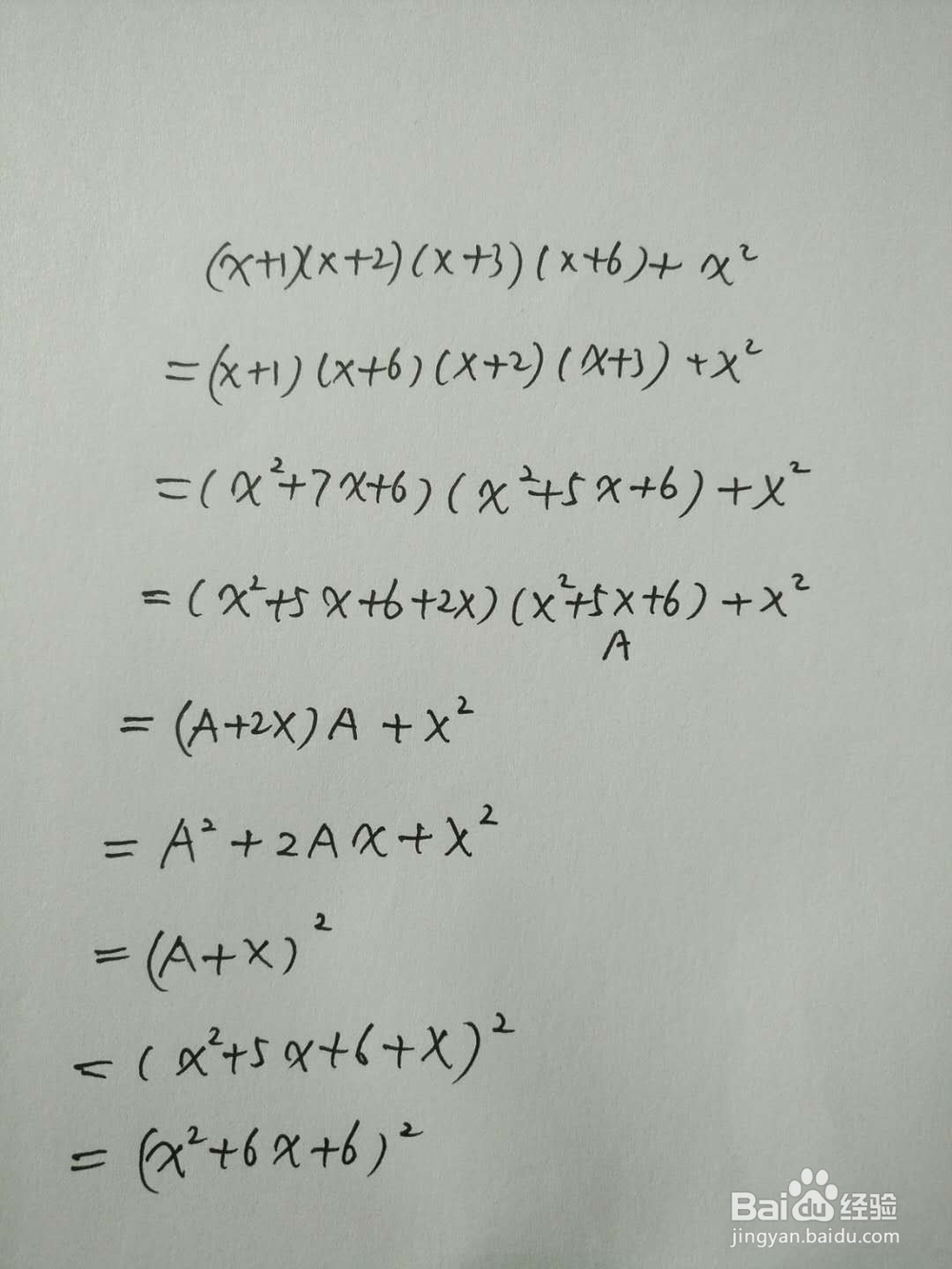因式分解的方法有很多,要根据因式的特征来选择方法,本经验主要介绍提取公因式、公式法、十字交叉法、换元法等方式进行因式分解。
工具/原料
代数式基本知识
数学公式
1.提取公因式法
1、这是因式分解的基本思路和方法,就是提取各因式的共同因数。
2、例如:xy+4x^2=xy+4*x*x=x(y+4x)
3、本例子先移项,然后分别提出m,n,再第二次提出公因式a+b.

4、本例子先提出前两项公因式2a,再提出后两项公因式b,最后再提出公因式x-5y。

2.公式法
1、公因式主要用到的公式如下:
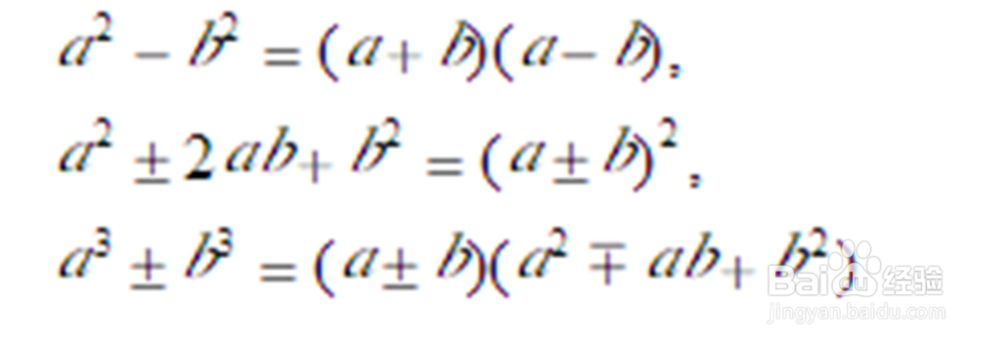
2、使用平方差公式举例:先提出公因式y,再使用公式。
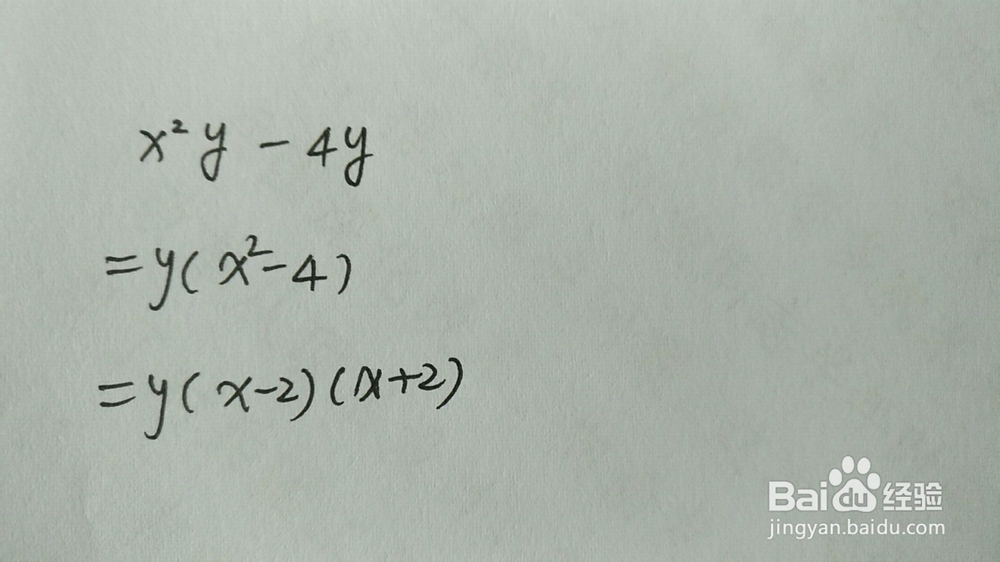
3、使用立方差公式举例:
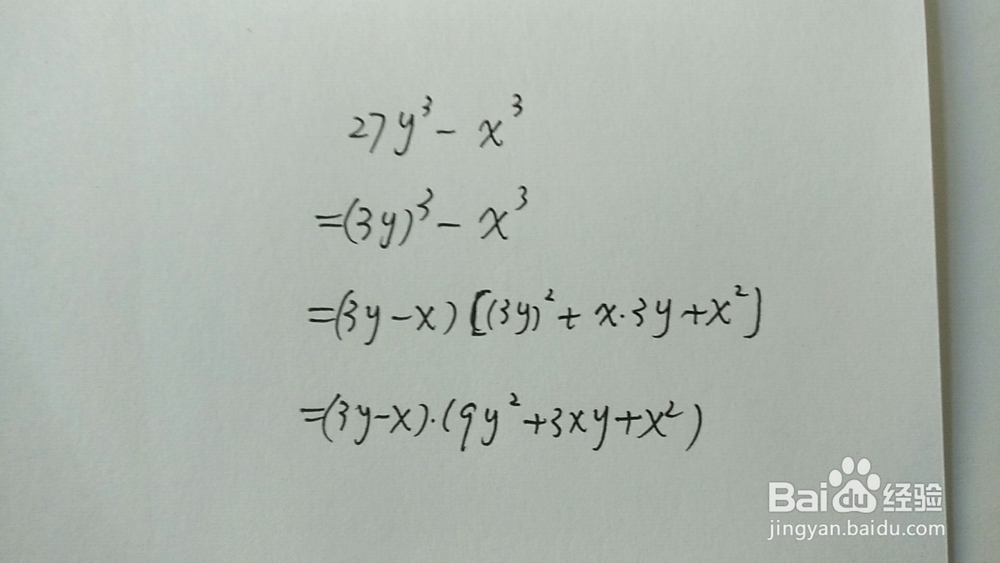
4、混合公式使用举例:先用到完全平方公式,后再用到平方差公式。
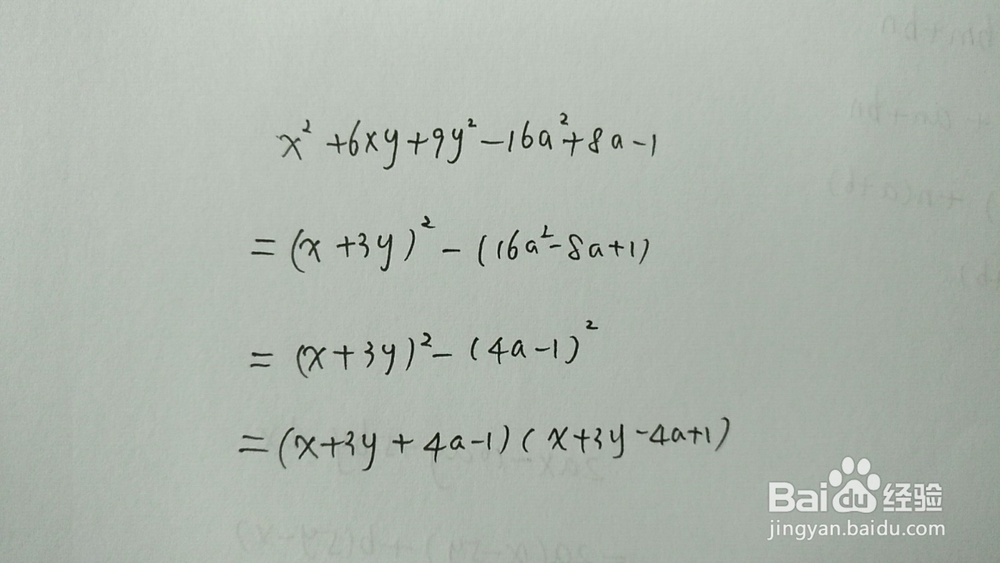
3.十字交叉法
1、此例子是把x+y看成一个整体,再十字交叉分解。
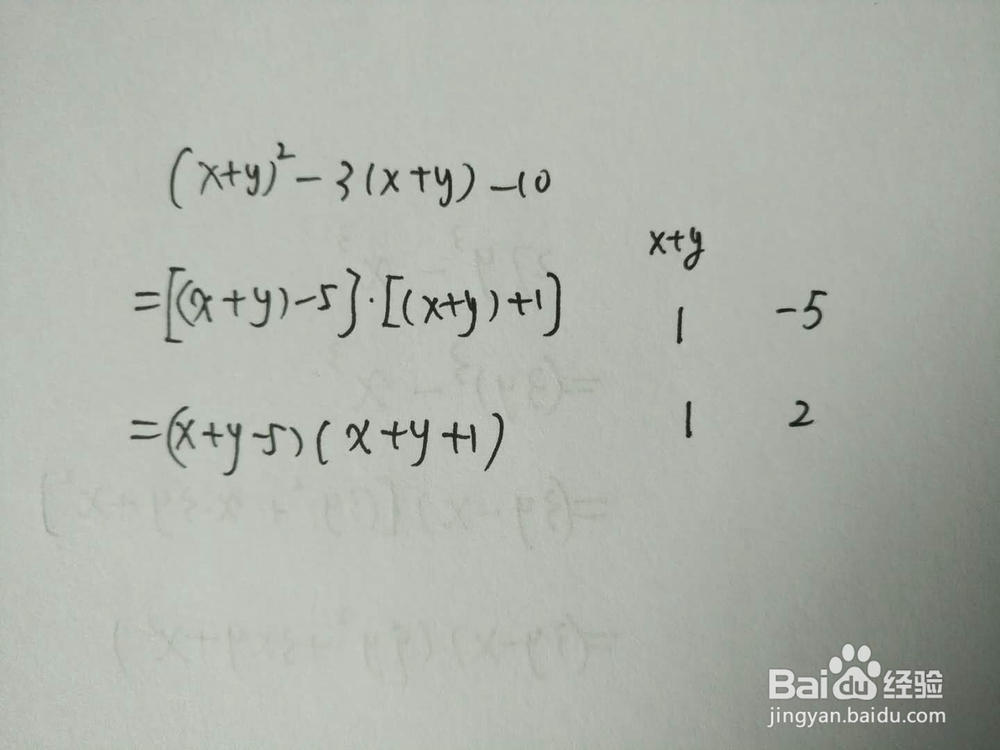
2、此例子是分别把x和y作为十字交叉的两方。
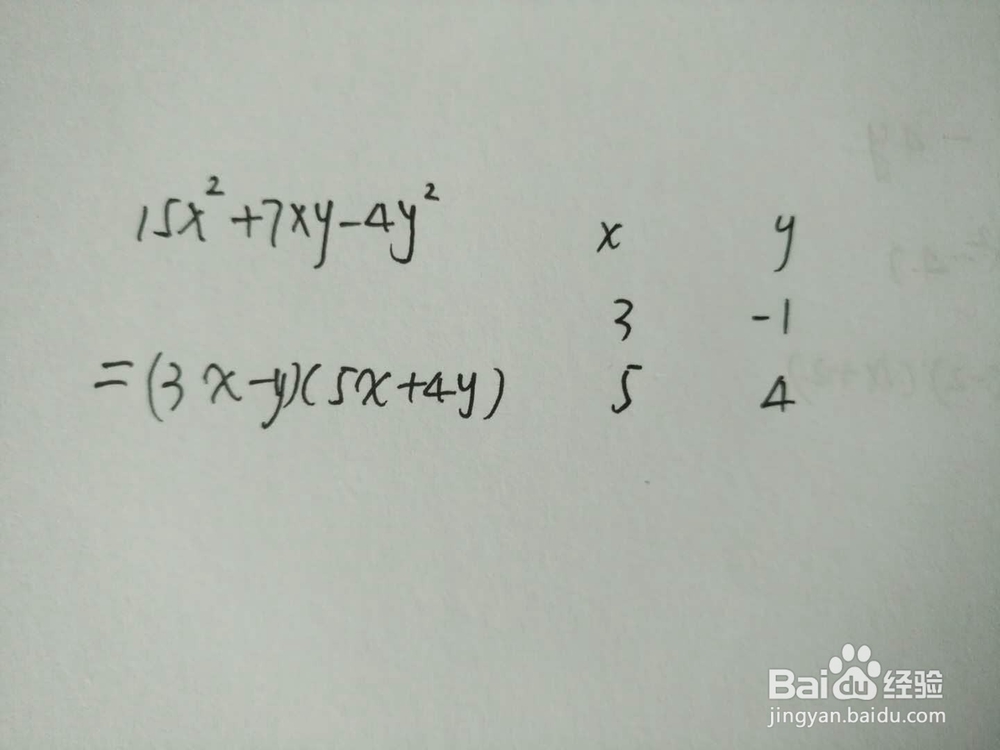
3、此例子是把x^3看成整体,再十字交叉。
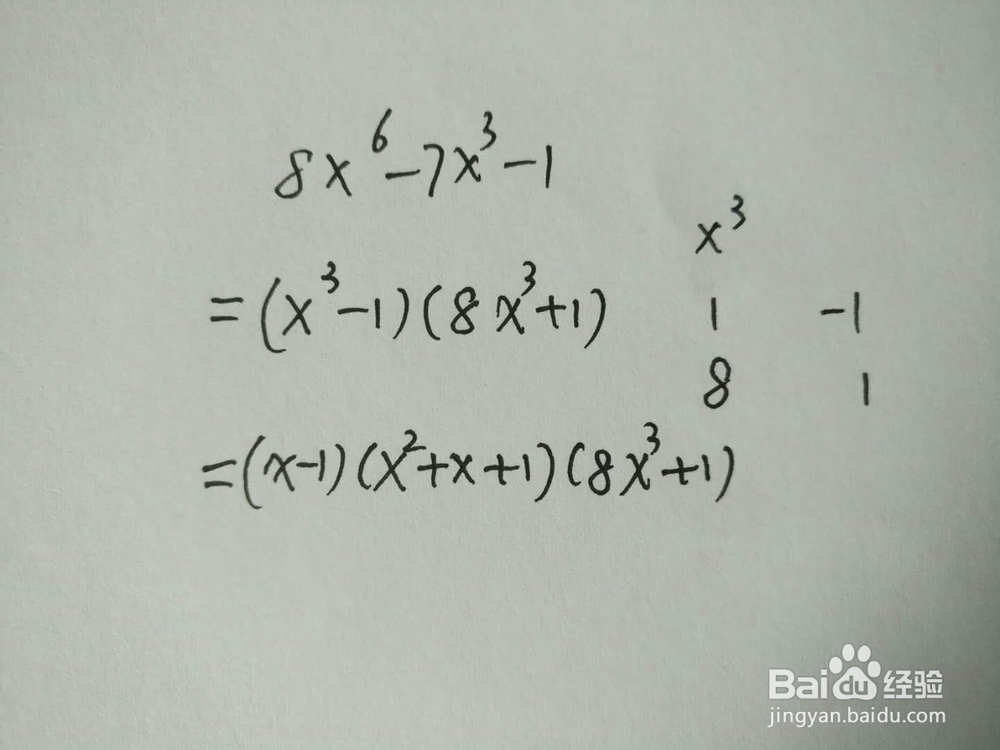
4.换元法
1、本例子中,先将因式移项并两迷撞笸痉两展开,再将相同的部分x^2+5x+6换元成A计算后因式分解,最后将A回换,即可得到最终结果。