1、Minkowski平面有两个维度,它的两个基本向量记为:e+=(1,0)e-=(0,i)其中的i是虚数单位。
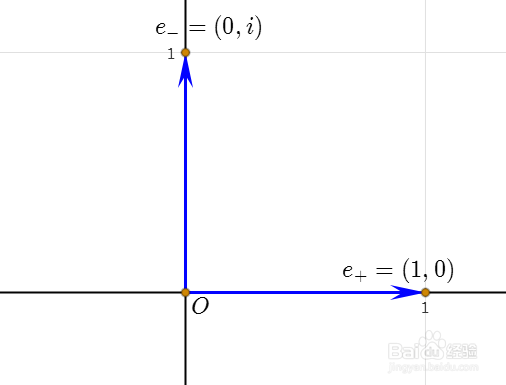
2、e-是一个奇特的向量,它与e+垂直,但是它的平方是负数。这里说的平方,指的是e-和e-的几何积。
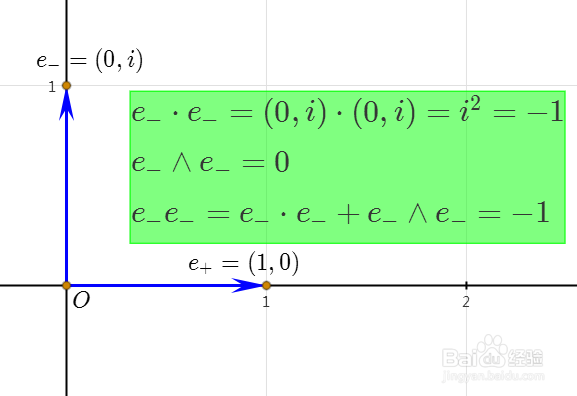
3、之所以把e-和e-的外积记为0,是因为两个共线的向量围成的"平行四边形"面积为0。

4、e+和e-的几何积等于二者的外积。注意到0乘以任何数字、双向量、多向量,都等于0,所以e+和e-的几何积的计算如下图。0与向量的乘积,是零向量,这一点很特别。

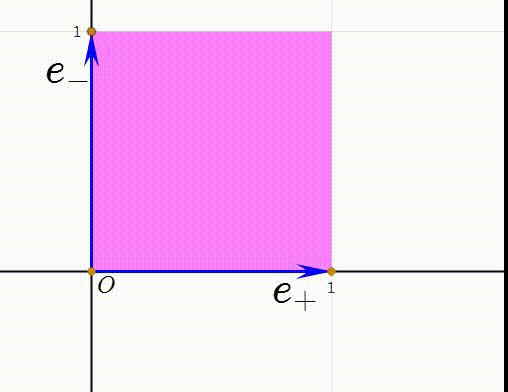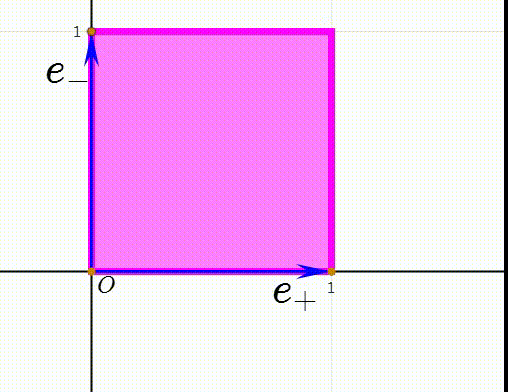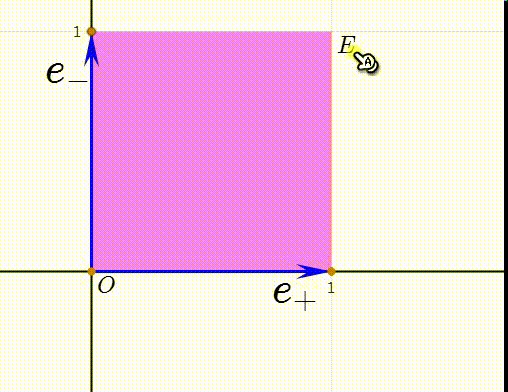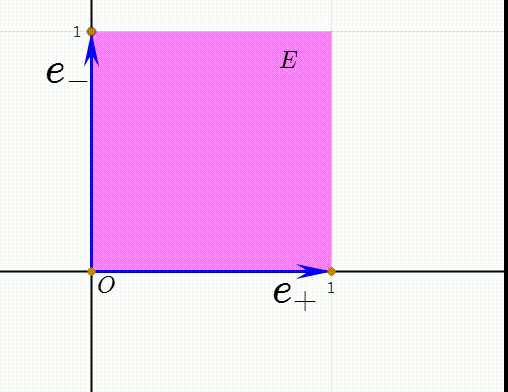
5、e+和e-的外积,是一个双向量,代表一个有向平面片的有向面积,我们把这个外积记为E。具体的,请参考《怎么正确理鞅瓞慈玢解向量的外积和几何积?》注意,E同样是Minkowski平面对应的几何代数空间里面的单位伪标量。
6、令e=e++e-,e0=(e--e+)/2,我们把e0和e称为Minkowski空间的空基(null basis)。
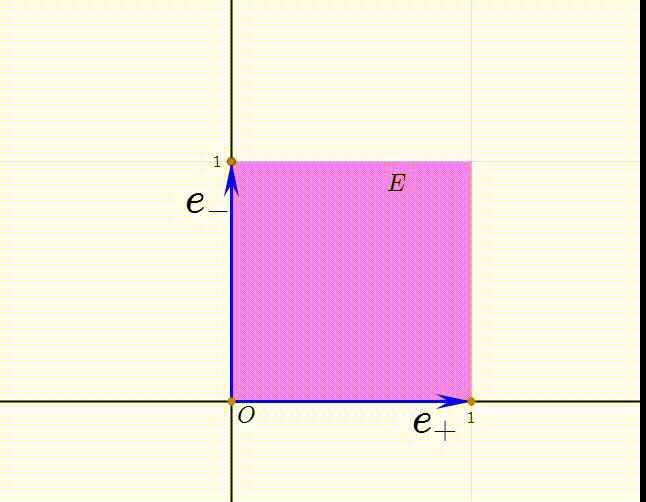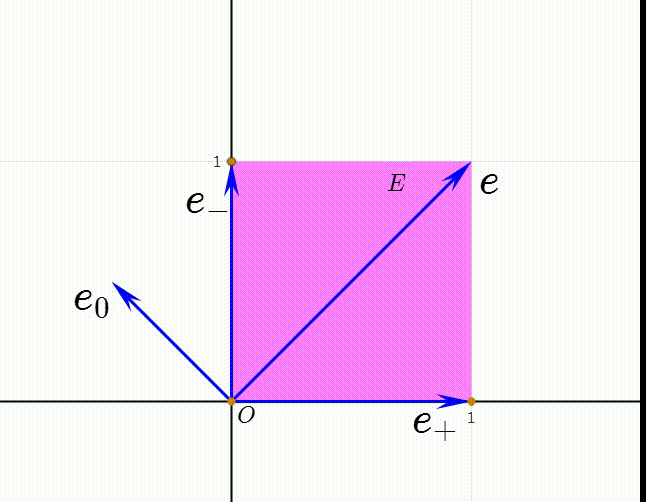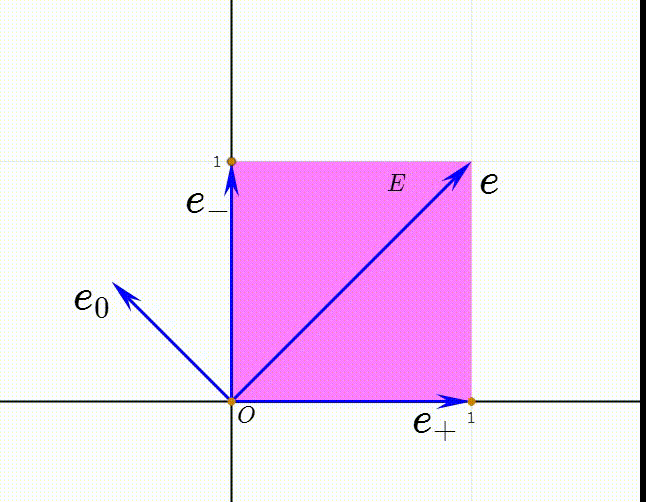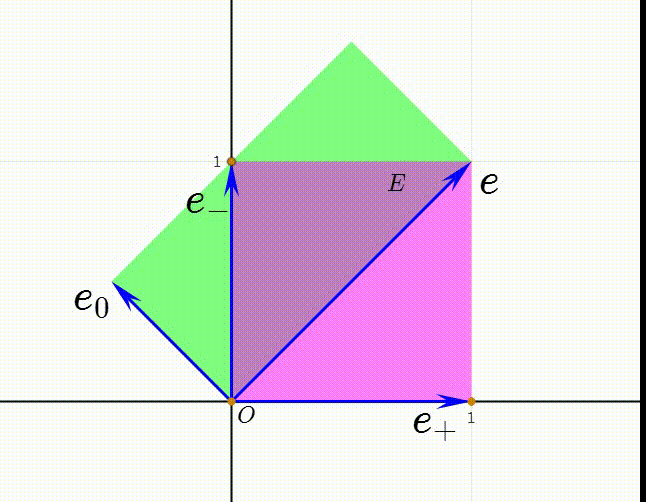
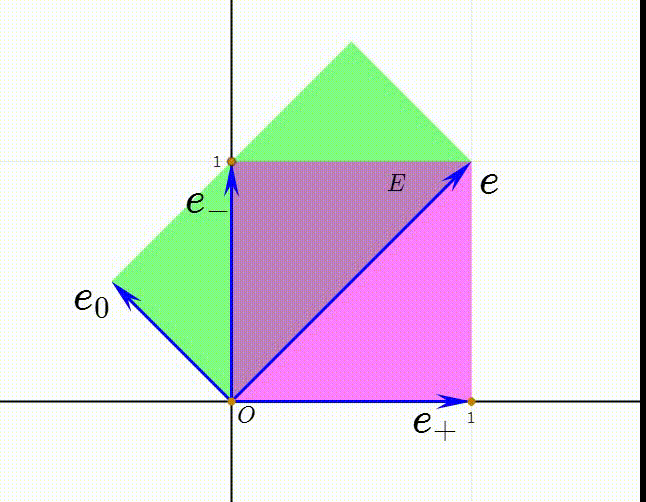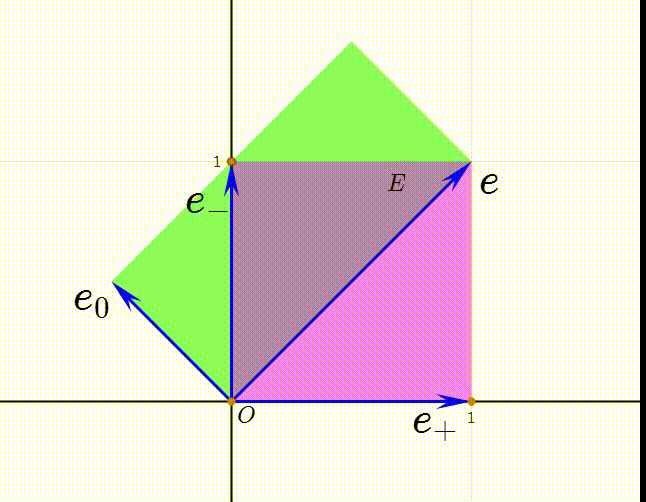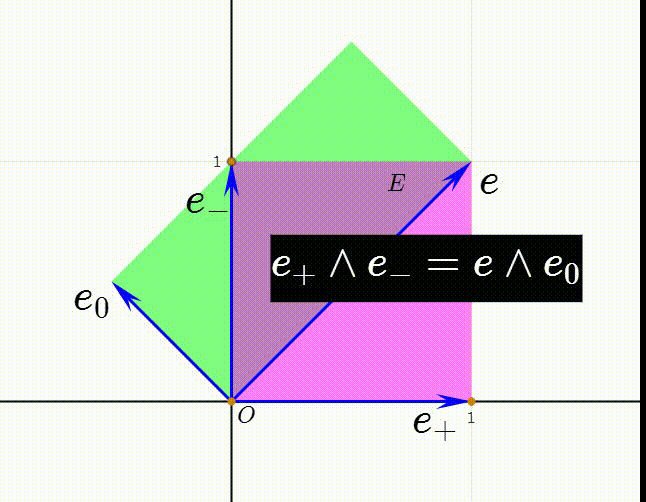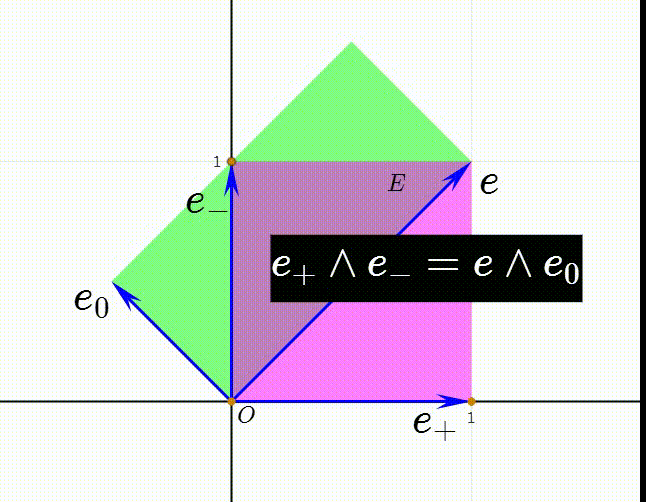
7、注意到两个长方形的面积相等,所以有:E=(e+)(e-)=(e+)∧(e-)=e∧e0