1、 把B、C分别置于(-1,0)和(1,0)的位置上,便于测量A的坐标。
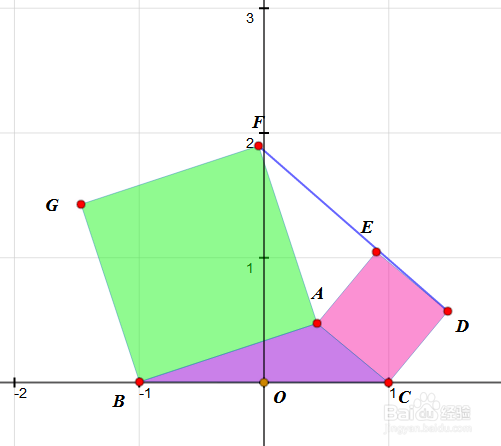
2、 测量A的坐标。如果不知道怎么测量点的直角坐标,请参考《网络画板基础——点和鼠标右键的用法》。
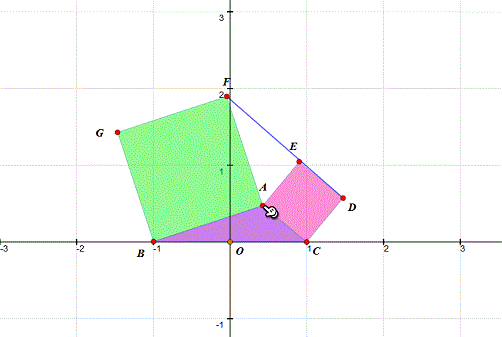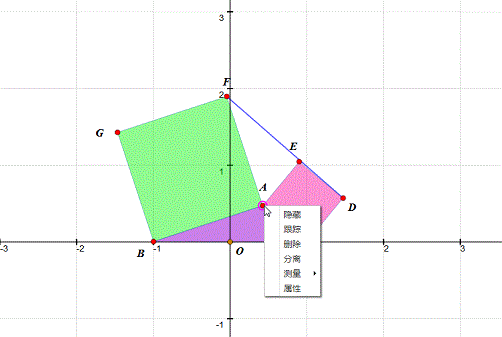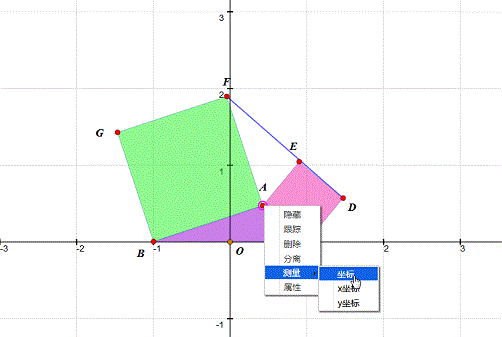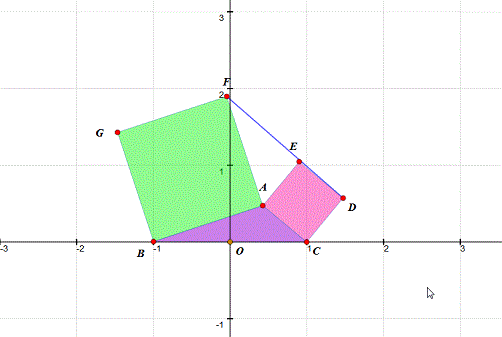
3、 测量△DEF的面积。当D、E、F共线,面积为0。这样,在观察的时候,一目了然!
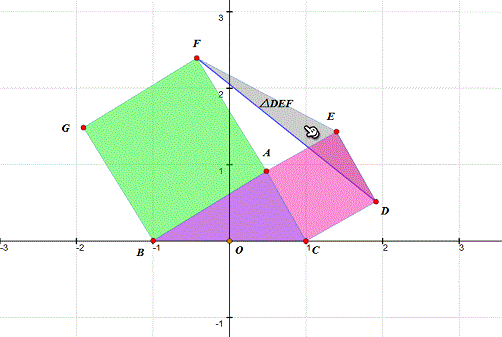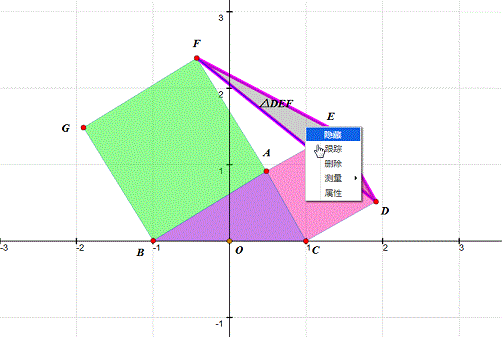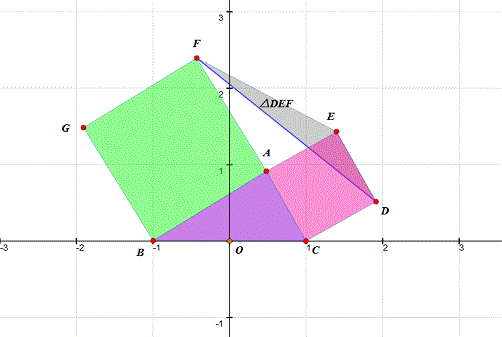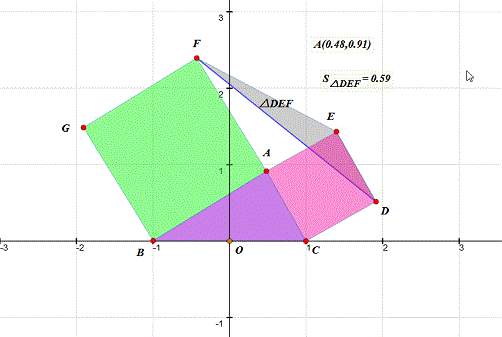
4、 拖动A,观察△DEF的面积为0的时候,记住A的坐标。 第一次得到的坐标是(0.53,0.50)(这是近似值,你的数据由你自己做主);再连续作四次拖动,把A的坐标都记下来。
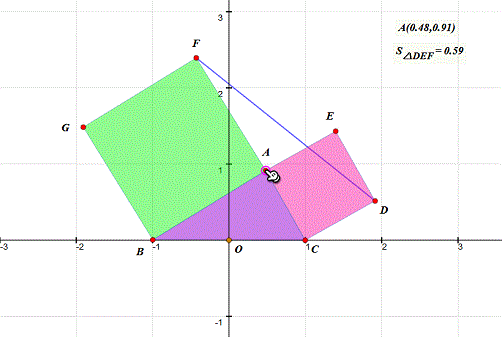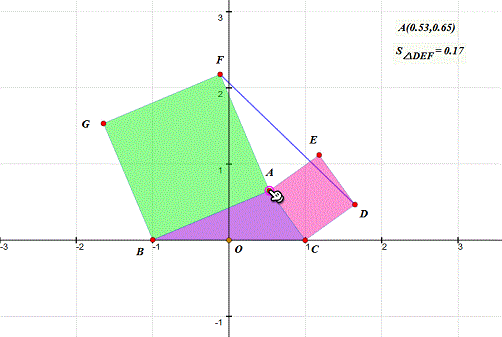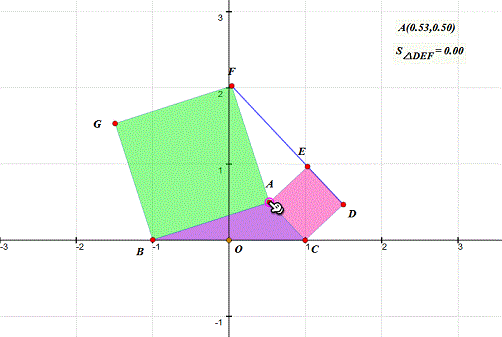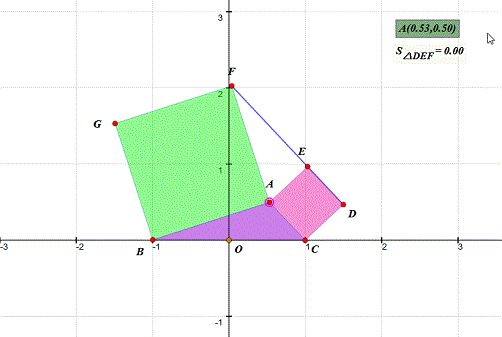
5、 把上面的坐标所代表的点画出来——没错,就是描点法——在难以构造A的轨迹的情况下,最快的方法就是描点法。 我找到的坐标是:(0.53,0.50)、(0.31,0.46)、(0.12,0.32)、(0.81,0.39)、(0.93,0.24)。
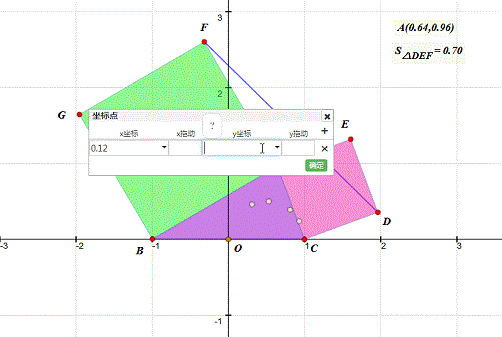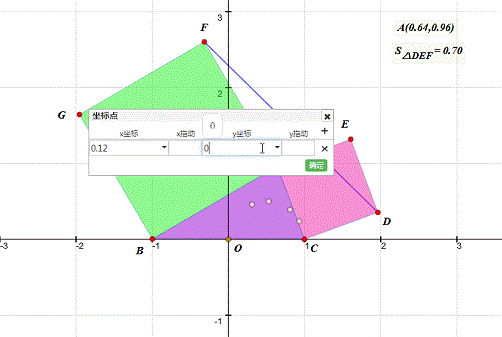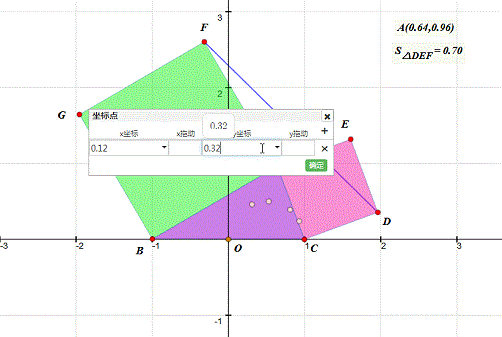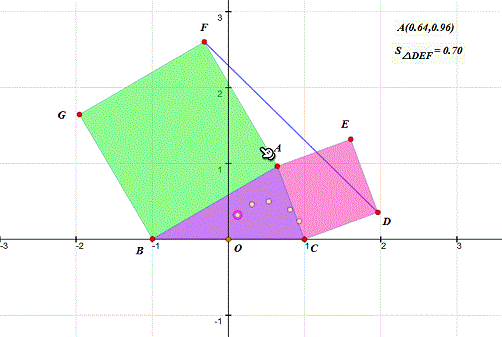
6、 观察这些点的位置,我们有理由猜测,A的轨迹应该是圆。而且,这个圆以BC的一半为直径。
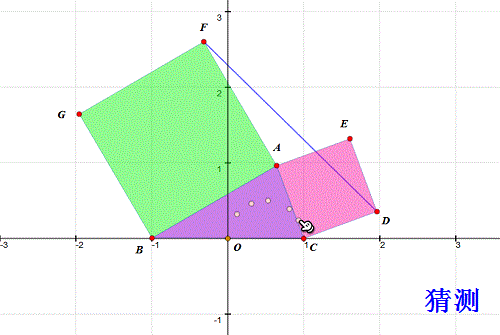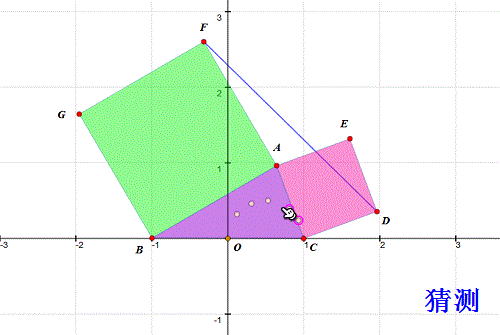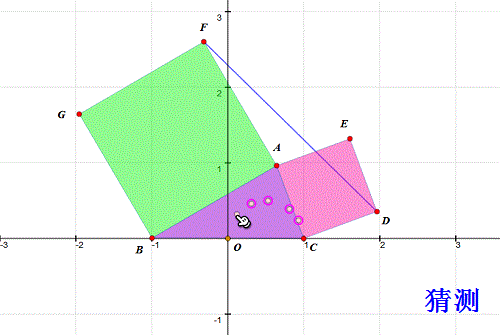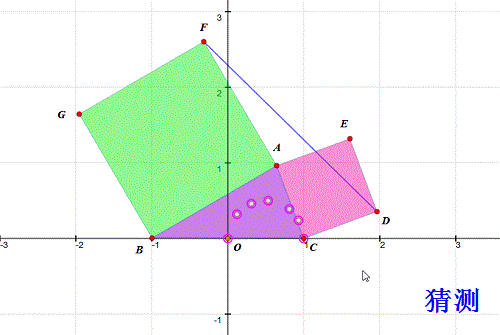
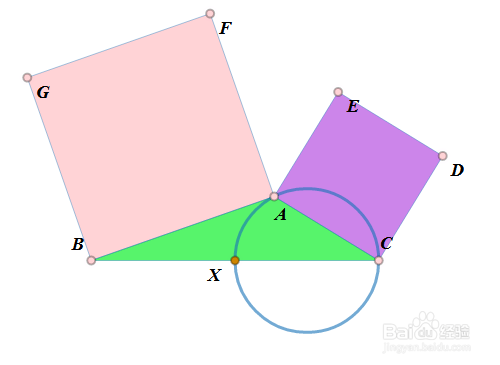
7、 做个实验验证一下(当然是另作图): 作B、C及其中点X; 以CX为直径作圆; 取圆上动点A; 分别用AB、AC向外作正方形ABGF、ACDE; 测量△DEF面积; 拖动A,观察面积是否变化! 结果,△DEF面积始终为0。
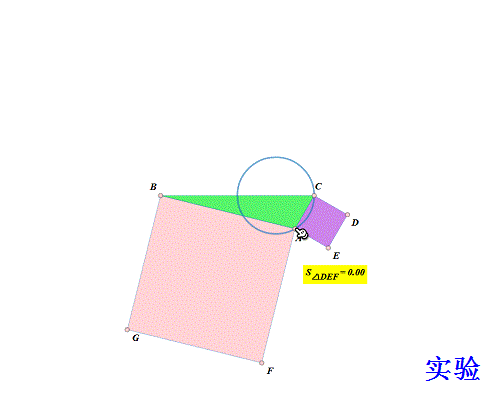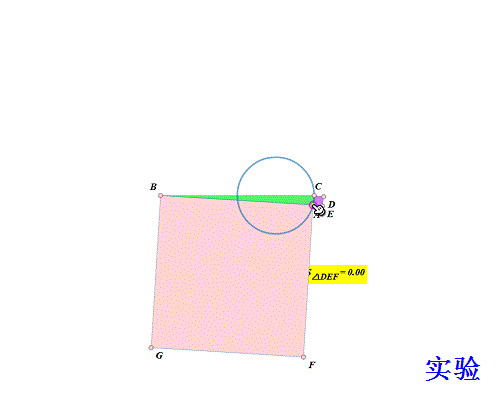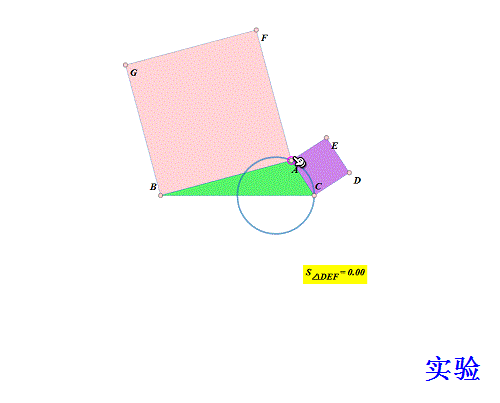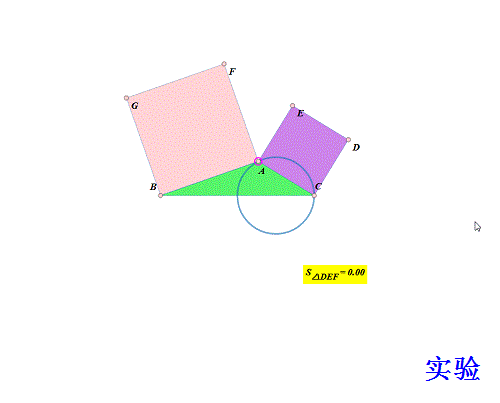
8、 所以,问题转化为证明题了: X为BC中点,以CX为直径作圆,A是圆上动点;分别用AB、AC向外作正方形ABGF、ACDE。求证:D、E、F共线。 这样,就比盲目地寻找A的轨迹容易多了!