1、函数为幂函数的乘积,则根据函数特征,自变量x可以取全体实数,定义域为:(-∞,+∞)。

2、确定函数的单调性,通过函数的一阶导数,判断函数y=(4x^2+1)(6x^2+2)的单调性。

3、如果函数y=f(x)在区间D内可导(可微),若x∈D时恒有f'(x)>0,则函数y=f(x)在区间D内单调增加;反之,若x∈D时,f'(x)<0,则称函数y=f(x)在区间D内单调减少。
4、通过函数的二阶导数,再根据二阶导数的符号,判断函数的凸凹性,进而解析函数y=(4x^2+1)(6x^2+2)的凸凹区间。

5、函数y=(4x^2+1)(6x^2+2)的极限,解析偶函数y=(4x^2+1)(6x^2+2)在无穷处的极限。

6、根据函数奇偶性判断规则,解析函数为偶函数。

7、根据定义域,结合函数驻点、拐点,列举函数y=(4x^2+1)(6x^2+2)五点图,函数部分点解析表如下:
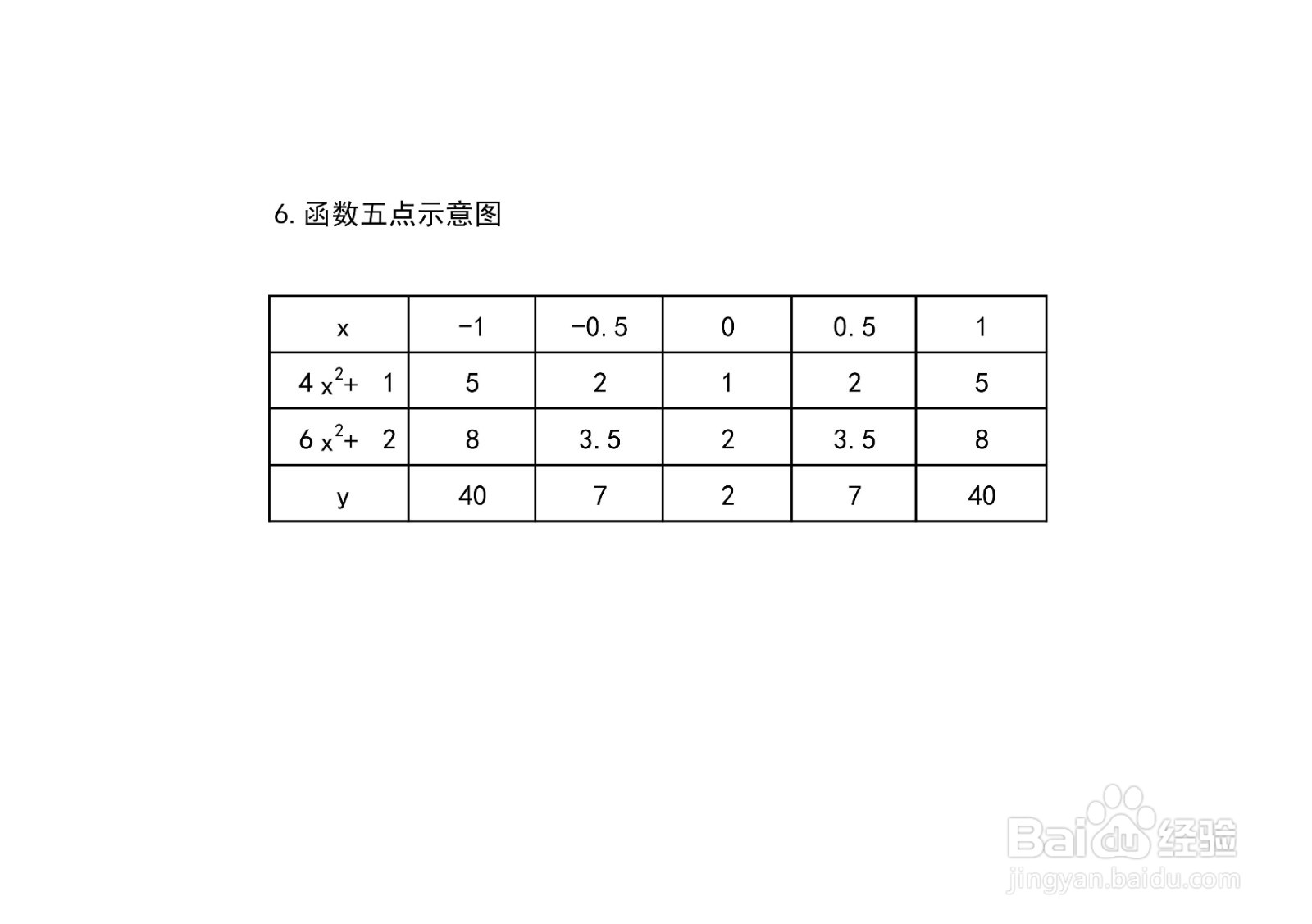
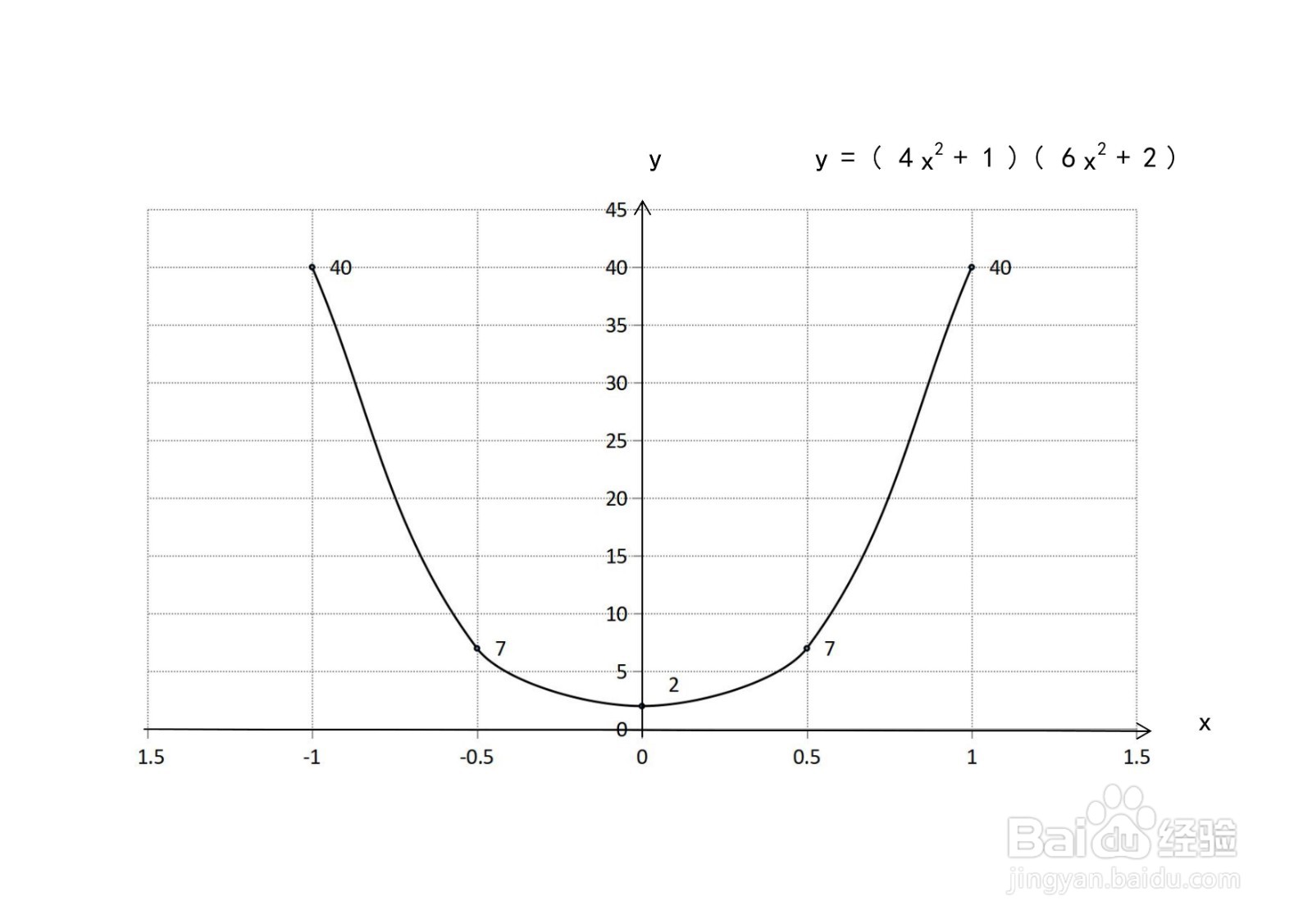
8、根据函数以上定义域、单调性、凸凹性、极限、奇偶性等性质,可画出二维坐标系画出y=(4x^2+1)(6x^2+2)示意图如下。