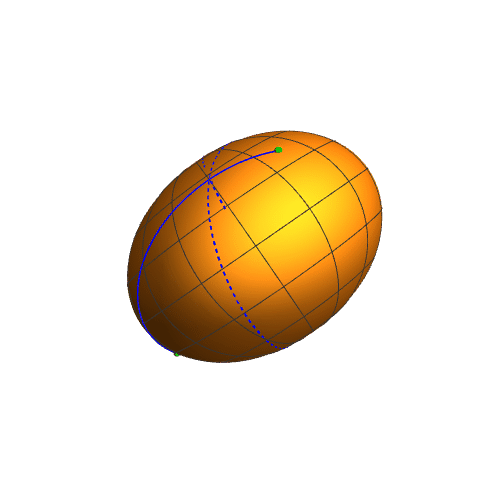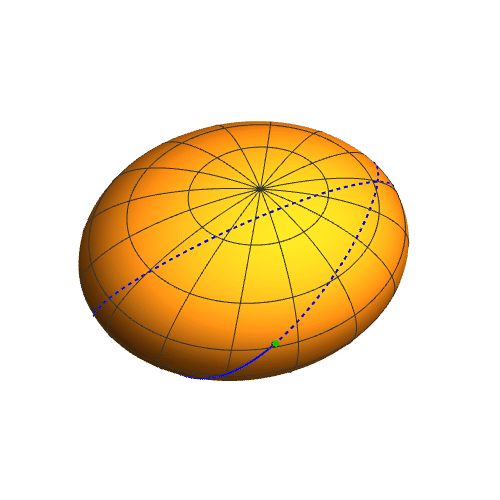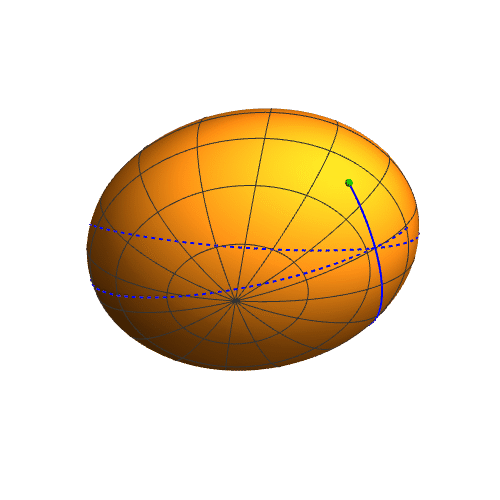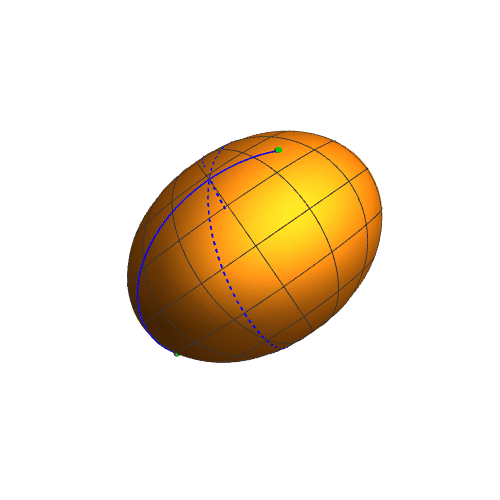1、给出一个具体的扁椭球:x^2/a^2+y^2/b^2陴鲰芹茯+z^2/c^2=1Mathematica可以直接用隐函数作图:ContourPlot3D[Evaluate[x^2/a^2 + y炷翁壳唏^2/b^2 + z^2/c^2 == 1 /. {a -> 5, b -> 4, c -> 3}], {x, -5, 5}, {y, -5, 5}, {z, -5, 5}, AspectRatio -> Automatic]
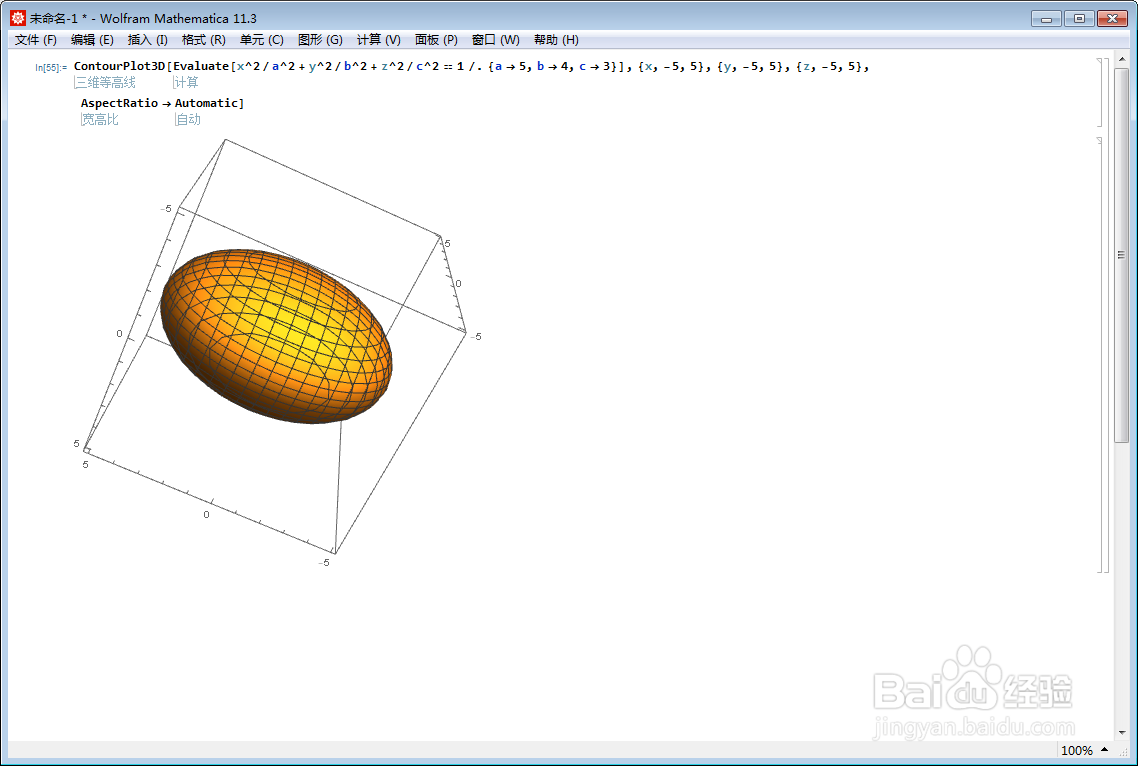
2、注意到,扁椭球可以通过球面仿射变换而得到,因此可以给出参数方程的作图方法:ParametricPlot3D[{5 Sin[u柯计瓤绘] Sin[v], 4 Cos[v] Sin[u], 3 Cos[u]},{u, 0, 2 Pi}, {v, 0, Pi}]

3、隐函数作图,没有明显的极化现象。上一个动态图,全面查看这个图形。
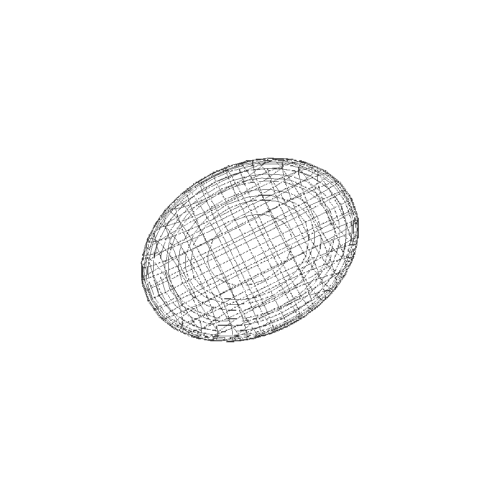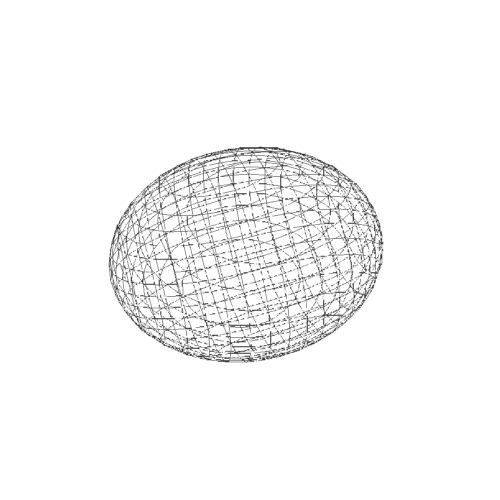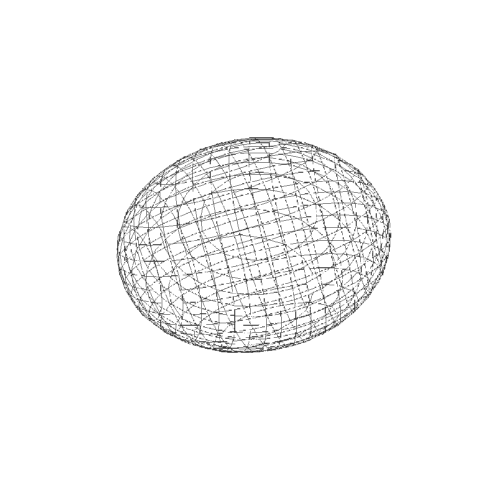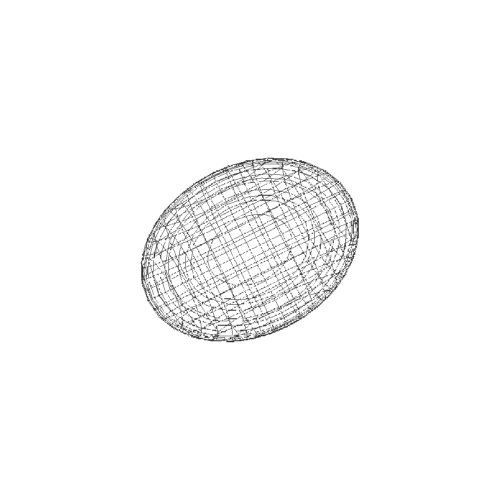
4、而参数方程作图,则出现明显的极化,经纬线分明。经线的集束点,就是极点。
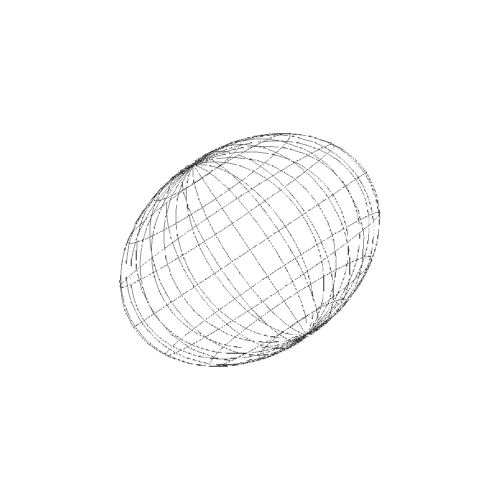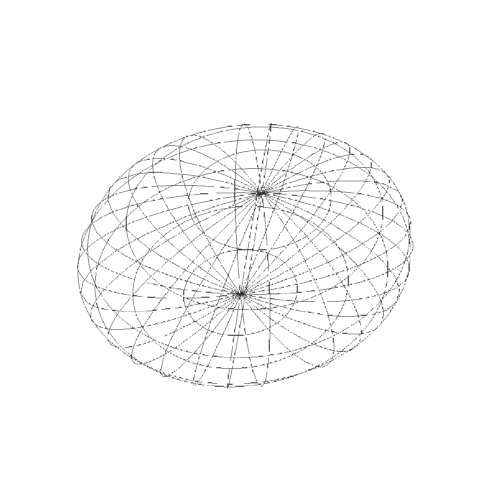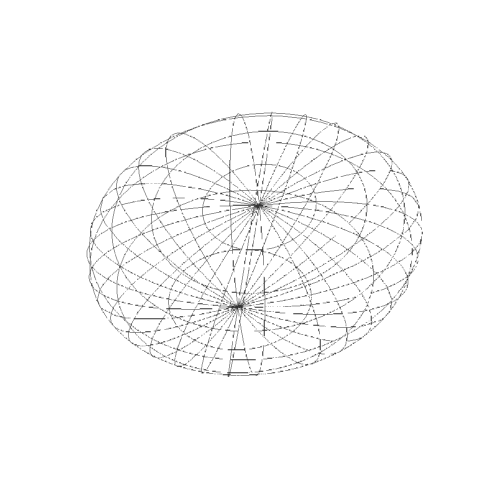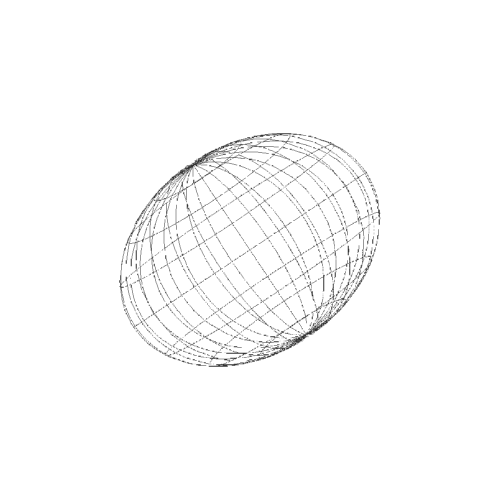
5、需要注意的是,扁椭球上面两点之间的短程线,不一定是平面曲线。
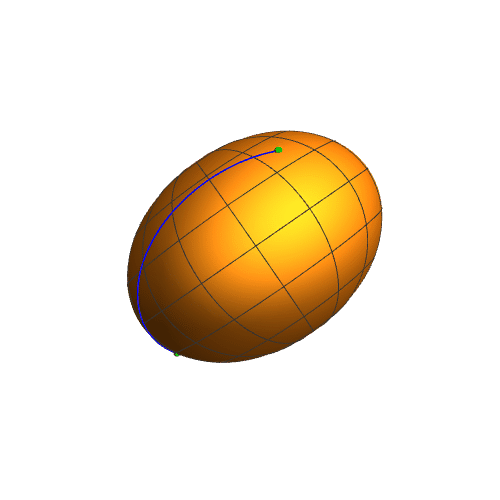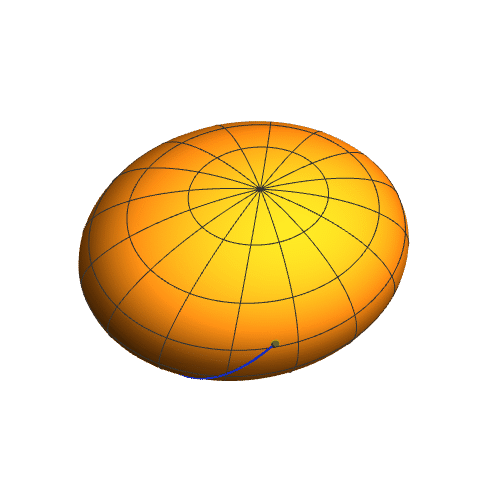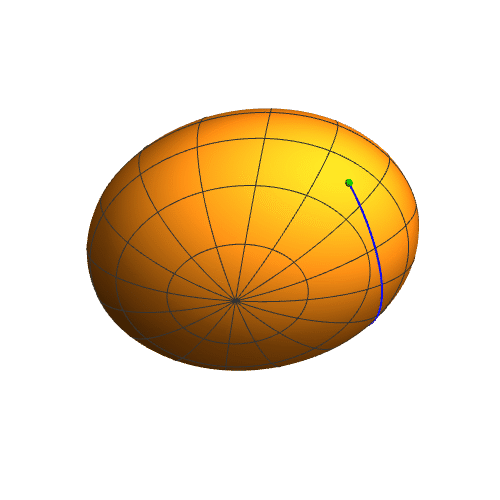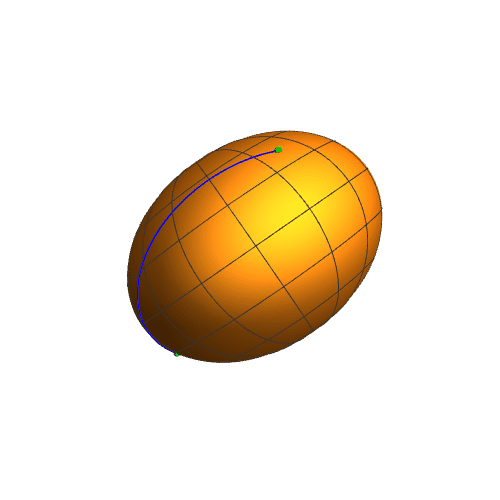
6、延长这条短程线,可以明显发现这不是一条平面曲线,看起来更像是扁椭球上面的缠绕线。