实数的加法群和正实数的乘法群怎么会同构呢?其实,同构的意思不是完全相同,而是指的是对应元素在群里面的地位是相同的。举一个不己首烈哆恰当的例子:狼群里面有头狼、狼兵,而蚁群里面也有蚁后和兵蚁,那么它们之间可以建立一种一一对应关系。同构,不仅要一一对应,还要保证,群元素之间相互作用的结果,也是对应关系。
工具/原料
电脑
实数的加法群
1、实数的加法群,指的是全体实数的集合,在加法规则下构成的群,它满足成为一个群的所有要求。

2、全体整数构成整数加法群,是实数加法群的子群。还可以有有理数加法群。

3、全体偶数也能构成一个群,可以称为偶数的加法群。这是整数加法群的子群,也是实数加法群的子群。除此以外,还有:3的倍数的加法群、n的倍数的加法群。

4、奇数集合不能构成加法群,因为里面没有单位元,而且不能保持封闭性。

正实数的乘法群
1、正实数的乘法群:单位元是1; 若x、y是正实数,那么,x*y是正实数。这保证了封闭性;可逆:x的逆元素是1/x。你能找出这个群的子群吗?

同构
1、设x是一个实数,那么2^x就是一个正实数,而且是一一对应的。

2、在这个规则下,x+y就对应着2^(x+y)=(2^x)*(2^y)。这说明,元素之间的相互作用也是一一对应的。
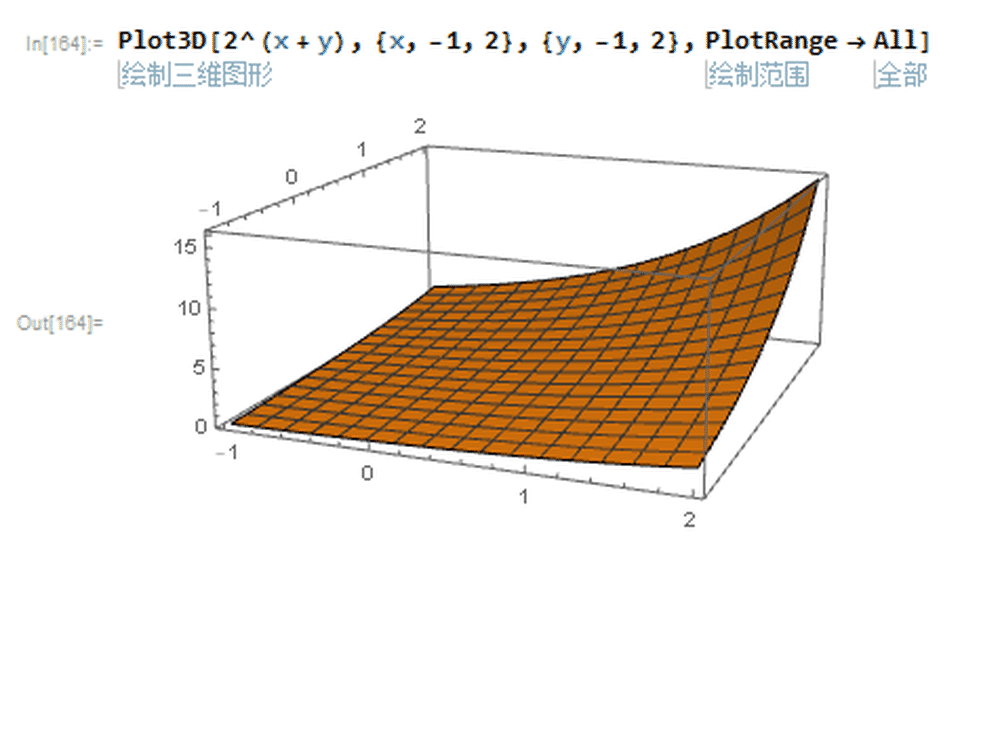
3、单位元也相互对应:1=2^0,0=Log[1]。综上所述,实数加法群和正实数乘法群确实是同构的。