本经验,通过函数的定义域、值域、单调性、凸凹性等性质,介绍画鲻戟缒男y=x^3+x^(-1)的图像的步骤。
工具/原料
函数基本性质
图像五点法
1.函数的定义域
1、 y=x^3+x^(-1),含有分式函数,则分母不为0。
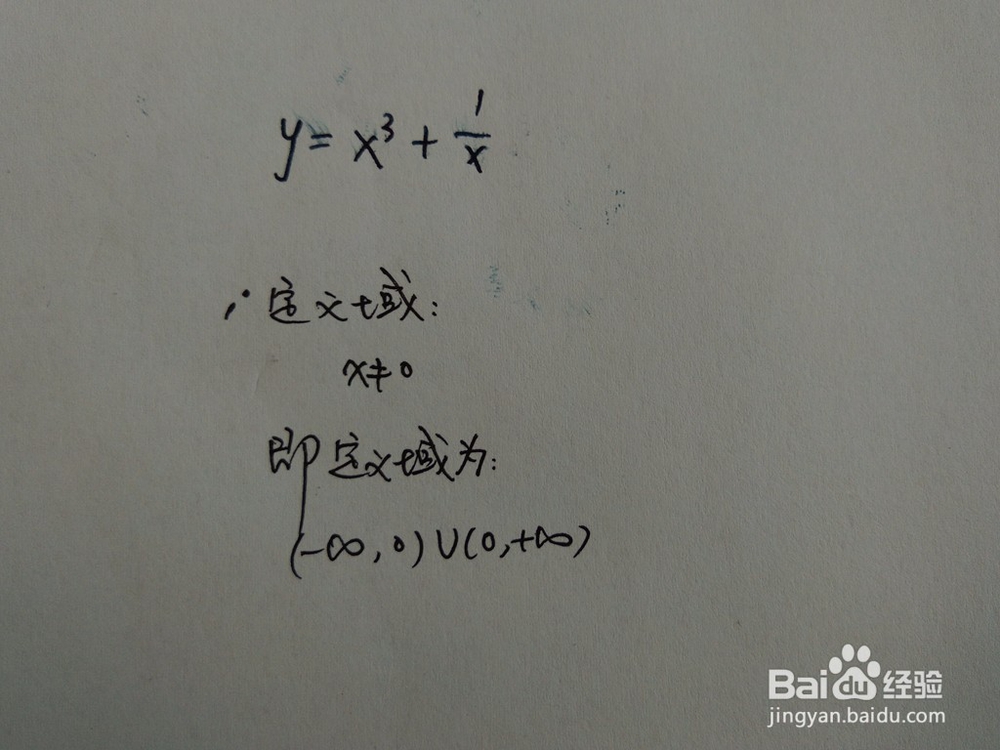
2.函数单调性
1、 用导数知识,通过函数的一阶导数,判断函数y=x^3+x^(-1)的单调性问题,求出函数的单调区间。
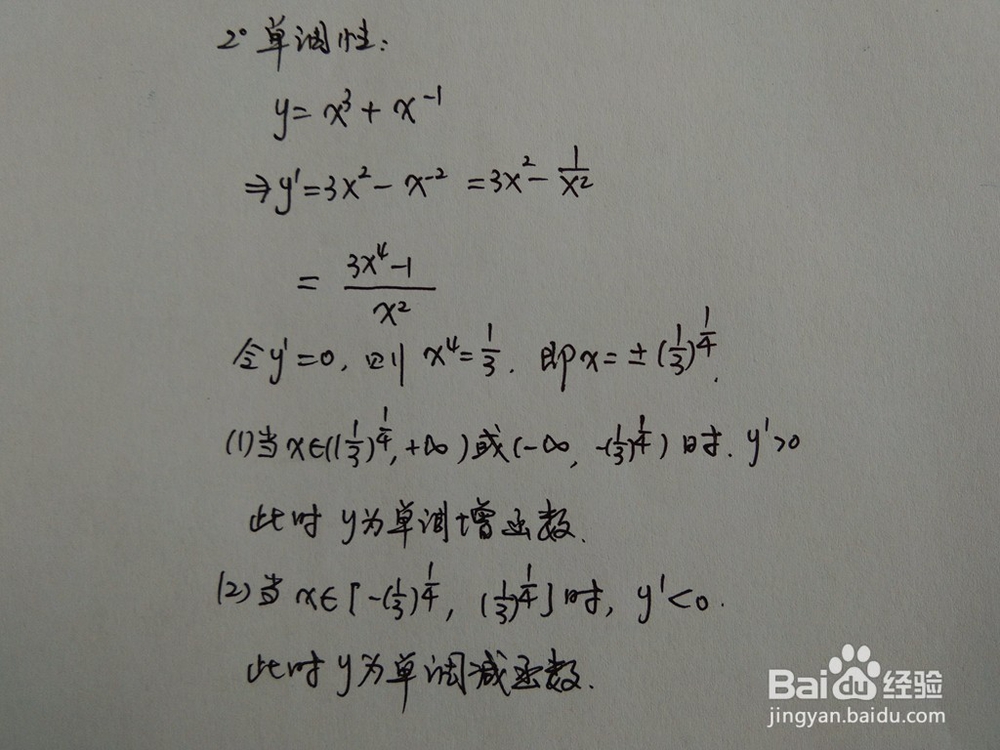
3.函数的凸凹性
1、 用导数知识,通过函数的二阶导数,判断函数y=x^3+x^(-1)的凸凹性,求出函数的凸凹区间。
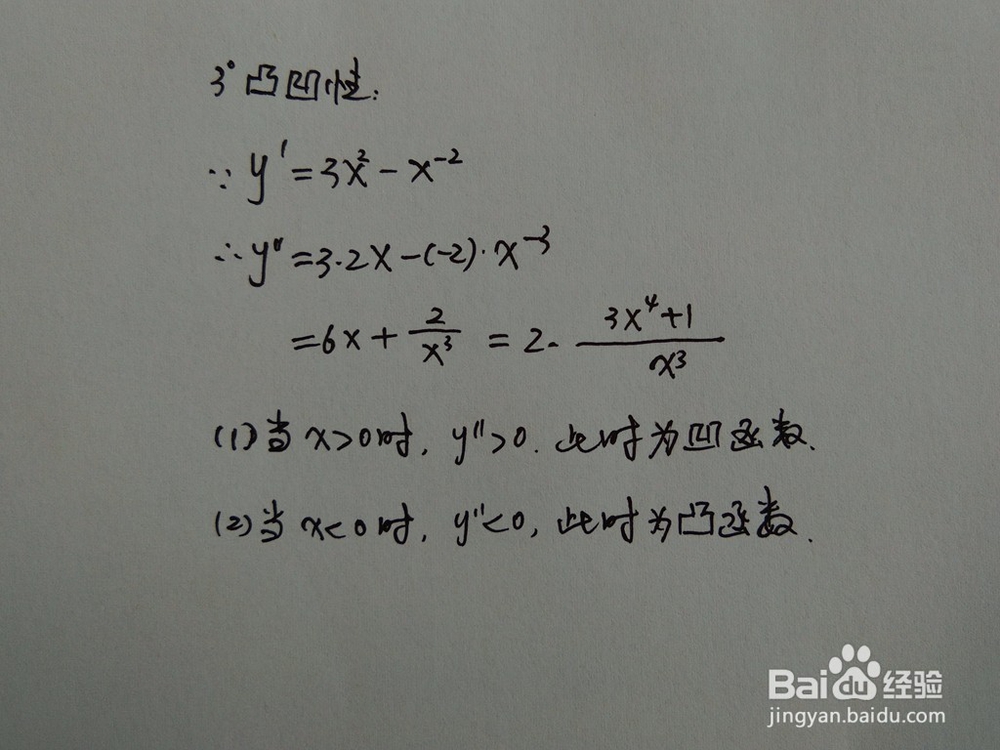
4.函数的极限
1、 本步骤介绍函数在正负无穷大及趋近于0处的极限。

5.函数的奇偶性
1、 本步骤为函数奇偶性判断步骤及过程。
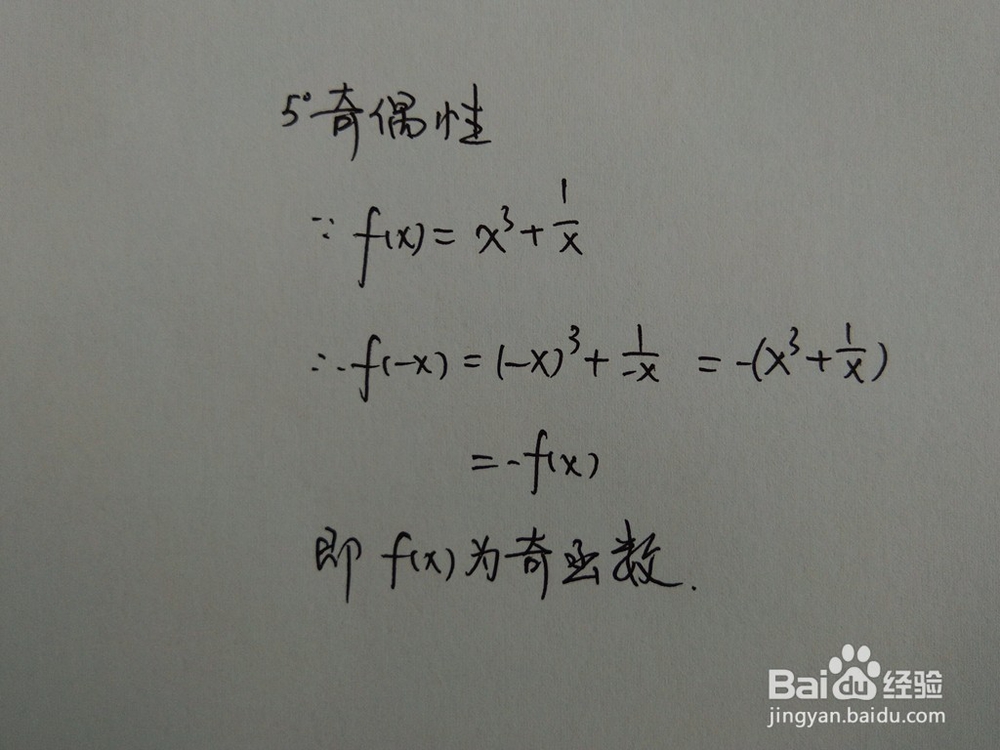
6.函数的极值
1、 根据函数的单调性,判断函数y=x^3+x^(-1)的极大值和极小值问题,并求出极大值和极小值。

7.函数五点图
1、 本步骤,介绍函数在定义域上五点图。
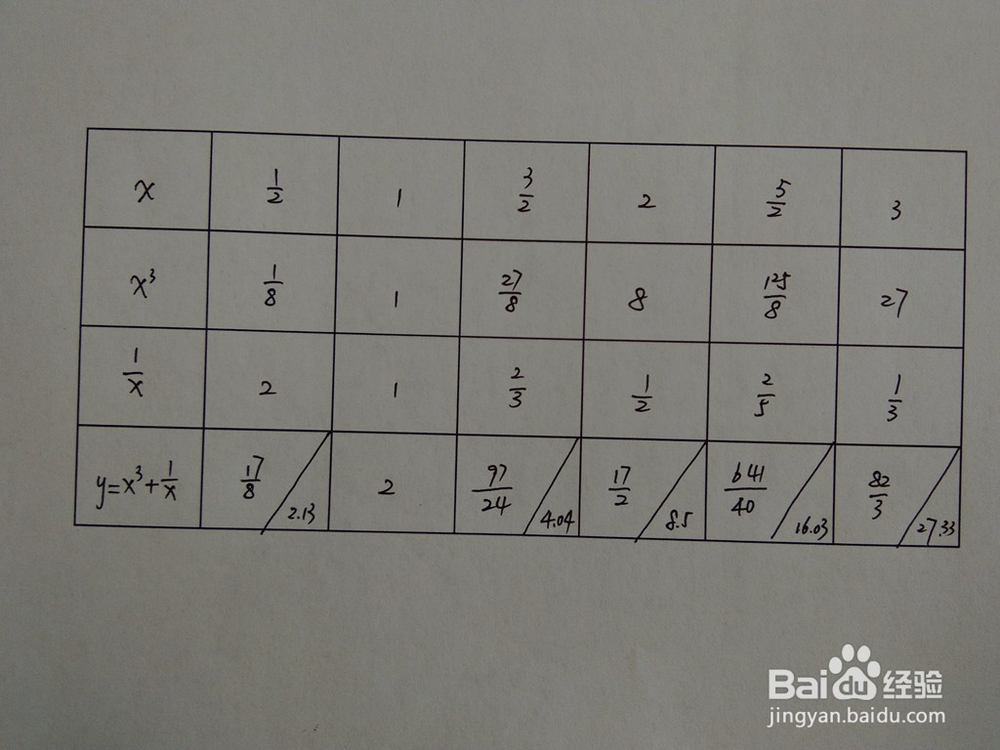
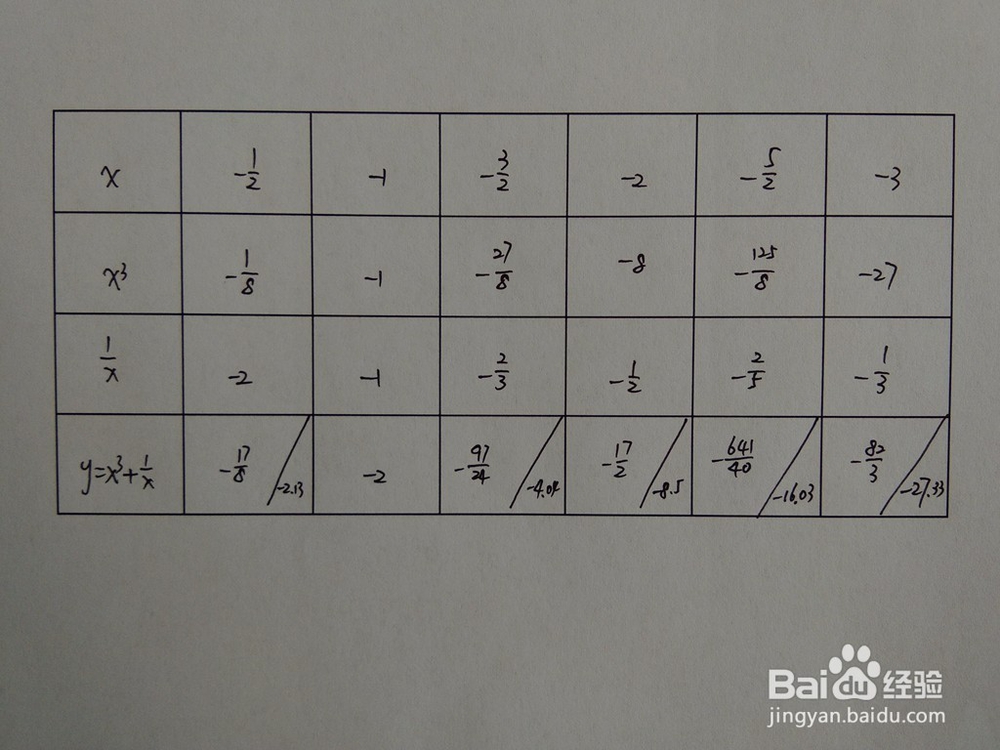
8.函数的示意图
1、y=x^3+x^(-1)在二维坐标系下的示意图。
