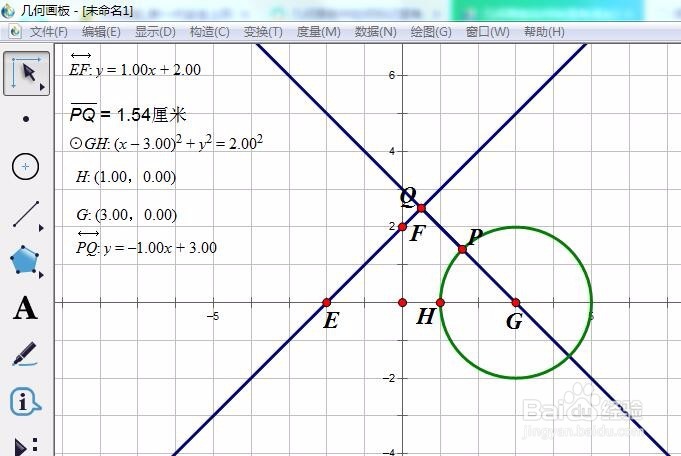
1、作出圆(x-3)^2+y^2=2^2作出直线y=x+2上作圆上一动点P到直线的垂线段PQ。
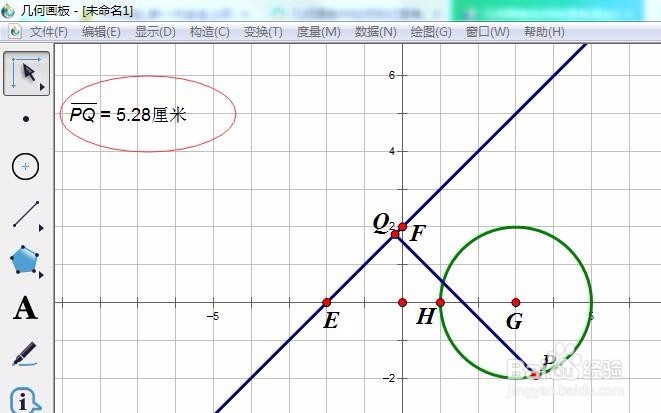
2、测量PQ的长度,如下图,5,28
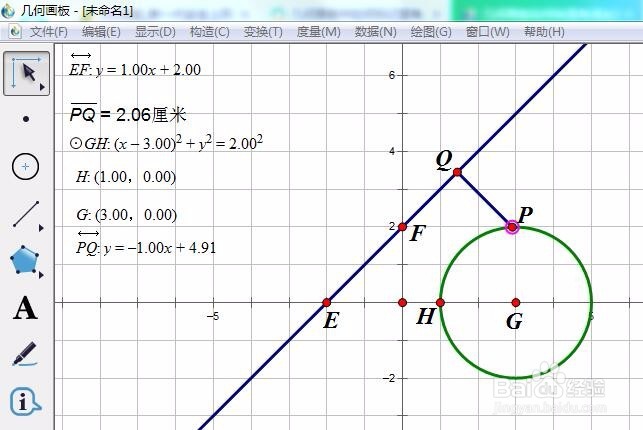
3、拉动P点在圆上运动。Q点相应移动,我们观察PQ长度变大,变小。
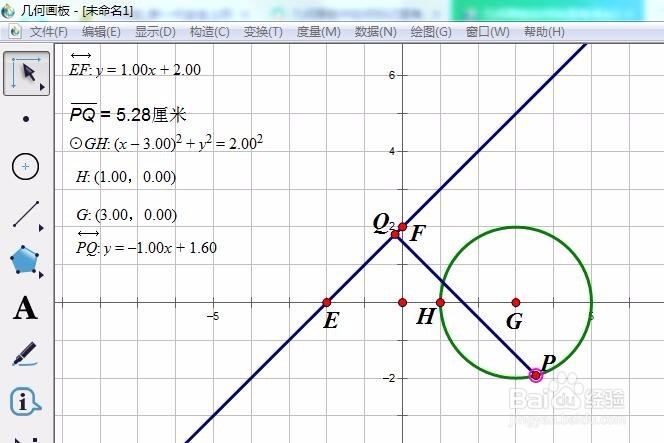
4、如下图,我们观察到P点在下图的状态时,PQ=5.54 为最大值。此时,PQ过圆心,且圆心是线段PQ的内分点。我们得到猜想PQ过圆心,且圆心是线段PQ的内分点时,PQ=5.54 为最大值。
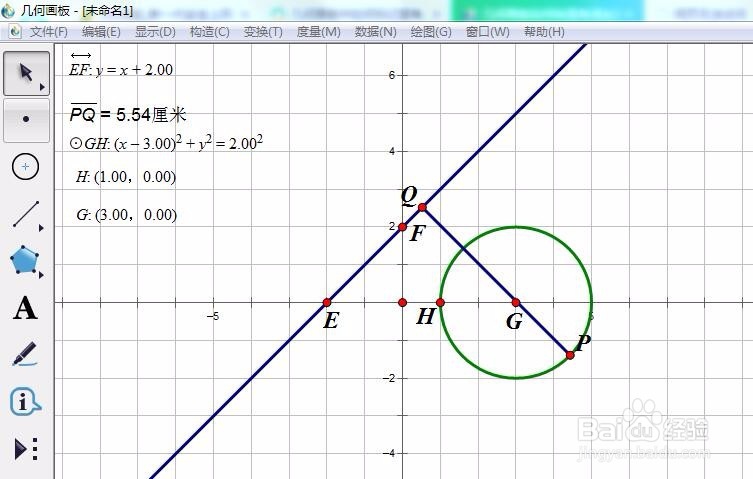
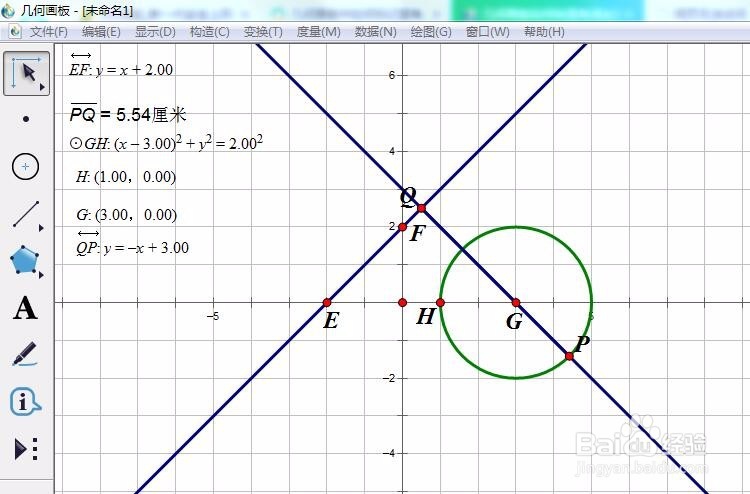
5、验证猜想:过圆心G作直线y=x+2的垂线,度量该直线的方程,得PQ:y=-x+3正好过P点。所以猜想成立。
6、类似第五步,得到猜想:Q=1.54 为最大值。此时,PQ过圆心,且圆心是线段PQ的外分点。我们得到猜想PQ过圆心,且圆心是线段PQ的外分点时,PQ=1.54 为最小值。
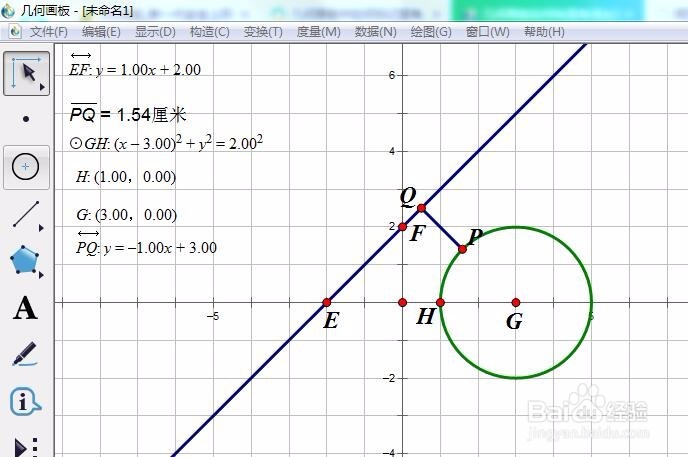
7、验证猜想:过圆心G作直线y=x+2的垂线,度量该直线的方程,得PQ:y=-x+3正好过P点。所以猜想好成立。