施密特正交化(Schmidt orthogonalization)是求欧氏空间正交基的一种方法。从欧氏空间任意线性无关的向量组α1,α2,……,αm出发,求得正交向量组β1,β2,……,βm,使由α1,α2,……,αm与向量组β1,β2,……,βm等价,再将正交向量组中每个向量经过单位化,就得到一个标准正交向量组,这种方法称为施密特正交化。
用数学归纳法可以证明:
设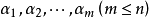 是
是 中的一个线性无关向量组,若令
中的一个线性无关向量组,若令

则 就是一个 正交向量组,若再令
就是一个 正交向量组,若再令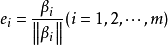
就得到一个标准正交向量组 ,且该向量组与
,且该向量组与 等价。
等价。
上述所说明的利用线性无关向量组,构造出一个标准正交向量组的方法,就是施密特正交化方法。
扩展资料
正交向量组是一组非零的两两正交(即内积为0)的向量构成的向量组。
几何向量的概念在线性代数中经由抽象化,得到更一般的向量概念。此处向量定义为向量空间的元素,要注意这些抽象意义上的向量不一定以数对表示,大小和方向的概念亦不一定适用。在三维向量空间中, 两个向量的内积如果是零, 那么就说这两个向量是正交的。正交最早出现于三维空间中的向量分析。 换句话说, 两个向量正交意味着它们是相互垂直的。若向量α与β正交,则记为α⊥β。