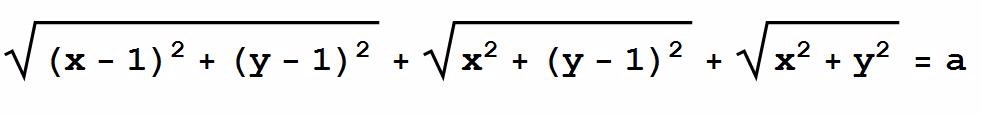1、Ω(2)的形状——桃仁 用Show命令把三个点(0,0)、(0,1)、(1,1)、Ω(2)画在同一个图里,代码如下:Show[Graphics[Point[{0, 0}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == 2, {x, 0, 1}, {y, 0, 1}]] Ω(2)有一个尖点位于B(0,1),形状像个桃仁!
2、Ω(2.136)——鼓起来的正三角形 代码:Show[Graphics[Point[{0, 0}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == 2.136, {x, 0, 1}, {y, 0, 1}]] Ω(2.136)把点B围在里面了,而A、C留在外面。看看,像不像因为膨胀而变形的正三角形?

3、Ω(1 + Sqrt[2])——有两个尖角 代码:Show[Graphics[Point[{0, 0}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == 1 + Sqrt[2], {x, -1, 1}, {y, 0, 2}]] Ω(1 + Sqrt[2])的两个尖角分别位于A点和C点处。 结合步骤一,作者发现,当曲线Ω(a)经过焦点时,会发生突变,不再光滑。不知道这是不是必然的!

4、Ω(2.569)——蒸好的馒头 代码:Show[Graphics[Point[{0, 0}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == 2.569, {x, -1, 2}, {y, -1, 2}]] 三个焦点都在曲线里面了。 你看看它像不像一个馒头? 注意看步骤一、二、三、四,作图区域发生变化了。

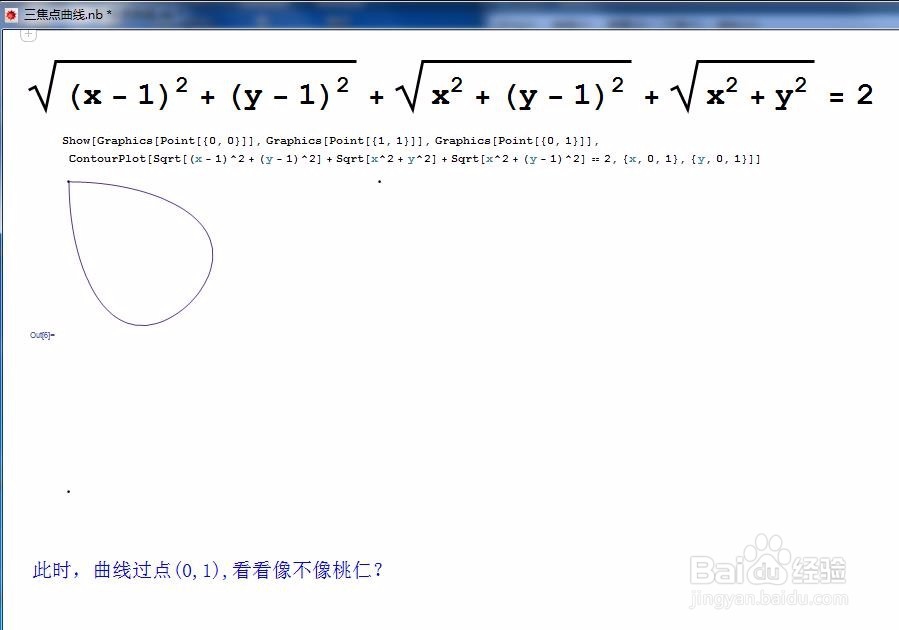
5、综合比较上面四幅图 复冠魂能爝杂的代码,是不被提倡的,因为这不仅输入费时,而且运行慢。尽量用简单的代码:Show[Graphics[Point[{0, 0}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],Table[ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == a, {x, -0.6, 1.3}, {y, -0.4, 1.5}], {a, {2, 2.136, 1 + Sqrt[2], 2.569}}]] 运行一下,就可以比较了。 注意作图区域,似乎不能够完全显示图形,但是图形却都显示的很完整。怎么回事呢?请自己思考!

6、更进一步 把A、B、C、a从1.93以0.009为间隔到2.59的图像,画在同一幅图里加以比较。 代码:Show[Graphics[Point[{0, 0魈胺闹臣}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],Table[ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == a, {x, -0.6, 1.3}, {y, -0.4, 1.5}, ContourLabels -> True], {a, 1.93, 2.59, 0.009}]] 慎入!如果你有密集恐惧症! a越大,图形的密度越大。 当曲线慢慢靠近A、C时,慢慢的显出了尖点。

7、 上面图中的中心区域的曲线密度有点稀疏,单独拿出来,以0.001为步长,重新画图:Show[Gr锾攒揉敫aphics[Point[{0, 0}]], Graphics[Point[{1, 1}]],Graphics[Point[{0, 1}]],Table[ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[x^2 + y^2] + Sqrt[x^2 + (y - 1)^2] == a, {x, 0, 1}, {y, 0, 1}, ContourLabels -> True], {a, 1.93, 2, 0.001}]] 运行以后,发现在这种情况下,当a越小,Mathematica越不能够很好的画出它的图形。
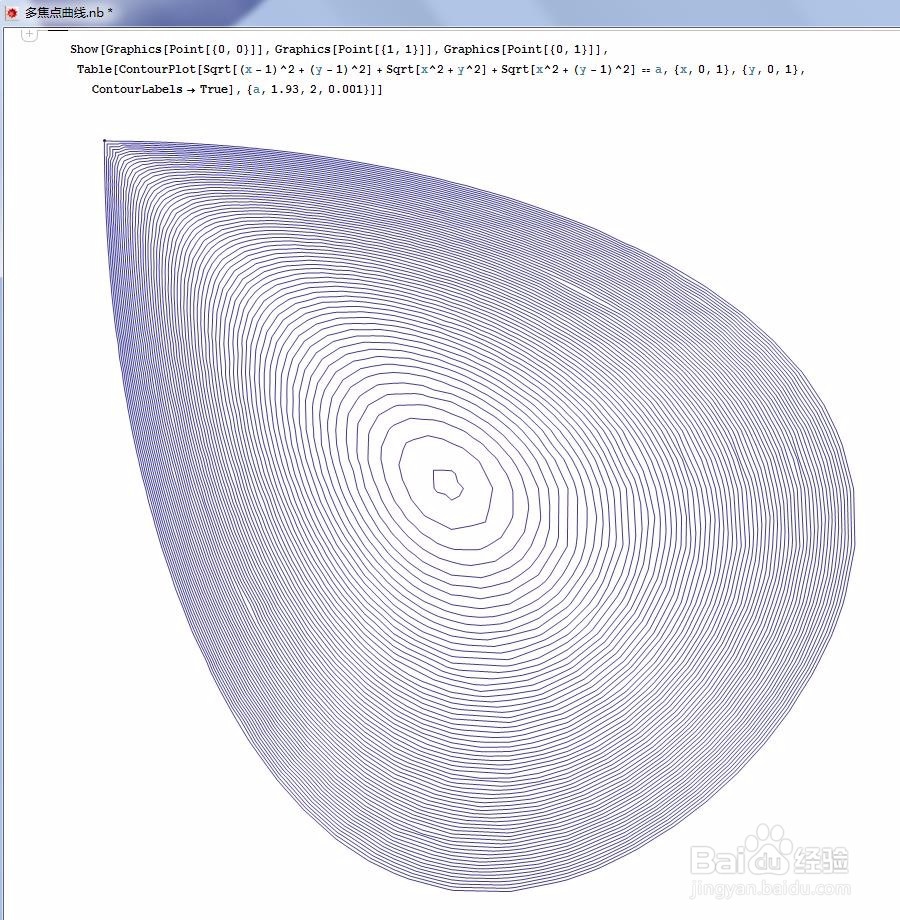
8、 于是,单独分开画图,看看当a趋近最小值的时候,能不能画出来? 代码:(请自行给a赋予具体的数值,在1.93和2.0之间,慢慢趋向于最小值)ContourPlot[Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[(x - 0)^2 + (y - 0)^2] + Sqrt[x^2 + (y - 1)^2] == a, {x, 0, 0.5}, {y, 0.5, 1}] 发现当a=1.932时,Mathematica已经不能精确地作图了! 这大概是Mathematica的一个缺点吧!
9、人机互动 把a的数值限制在1 .93到2 .59之间,变换速率是0 .001.这样的话,如果导出为动态掬研疔缎图,那么帧数=((2.59-1.93)/0.001)=660.如果你想用Mathematica把这个动态图导出来,请参考《怎么用Mathematica制作动态图片》。 互动程序的代码如下:Manipulate[ContourPlot[ Sqrt[(x - 1)^2 + (y - 1)^2] + Sqrt[(x - 0)^2 + (y - 0)^2] + Sqrt[x^2 + (y - 1)^2] == a, {x, -1, 2}, {y, -1, 2}], {a, 1.93, 2.59, 0.001}] 拖动滑块到a=2,图形像个桃种;a=2.136,图形像个膨胀变形的正三角形;a=2.398,图形好像出现了两个尖尖角,不光滑了;a=2.569,图形好像个馒头;............。
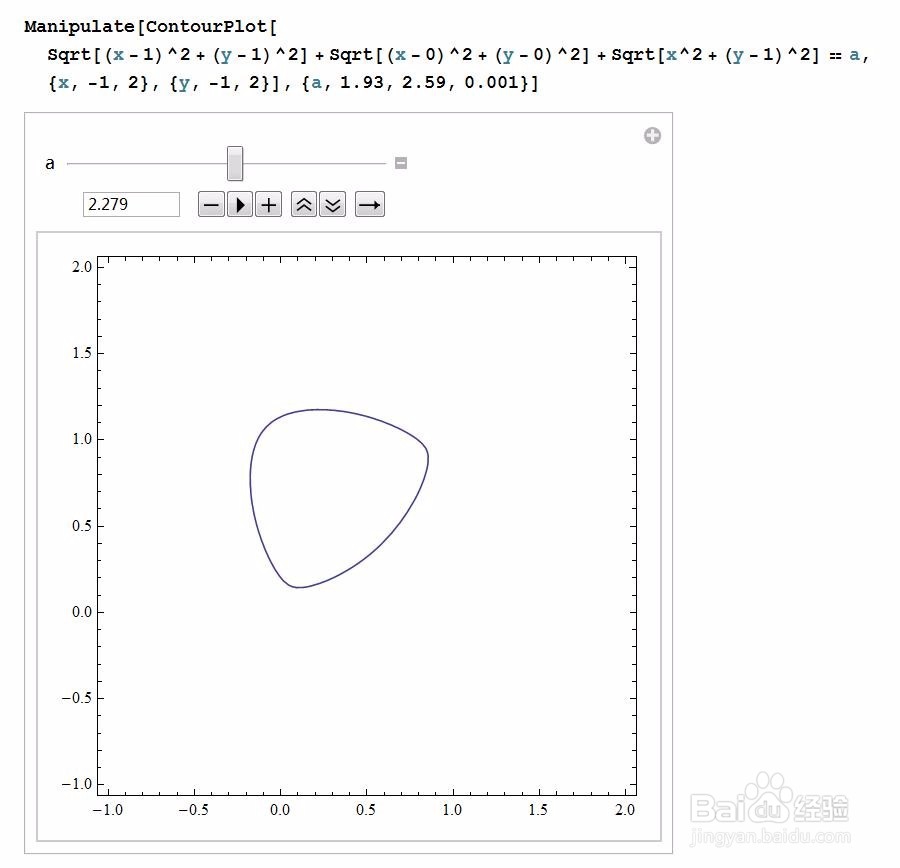
10、a的最小值 事实上,当a最小,Ω(a)退化成一个点,没错,就是△ABC的Fermat点。
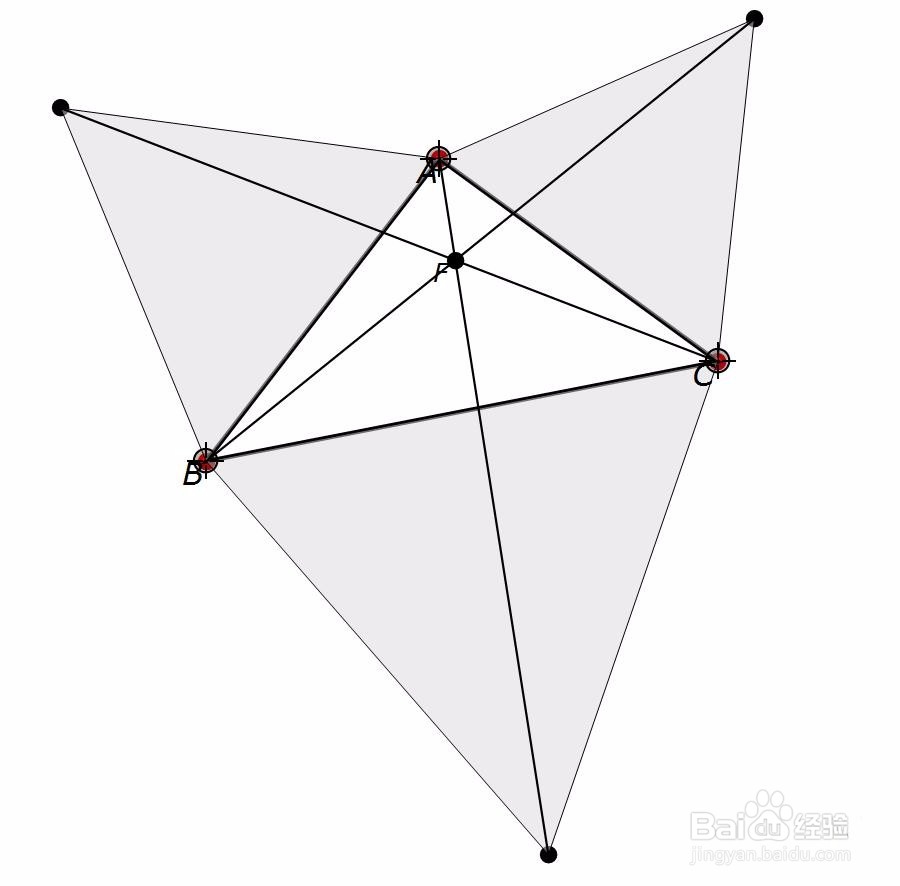
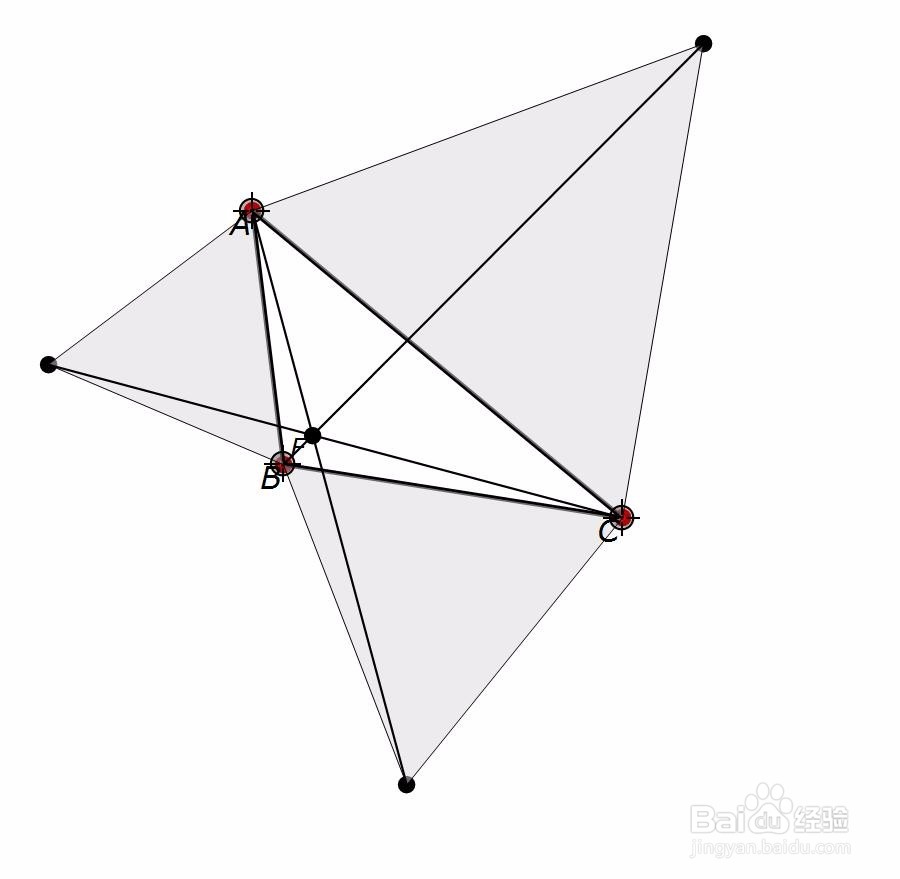
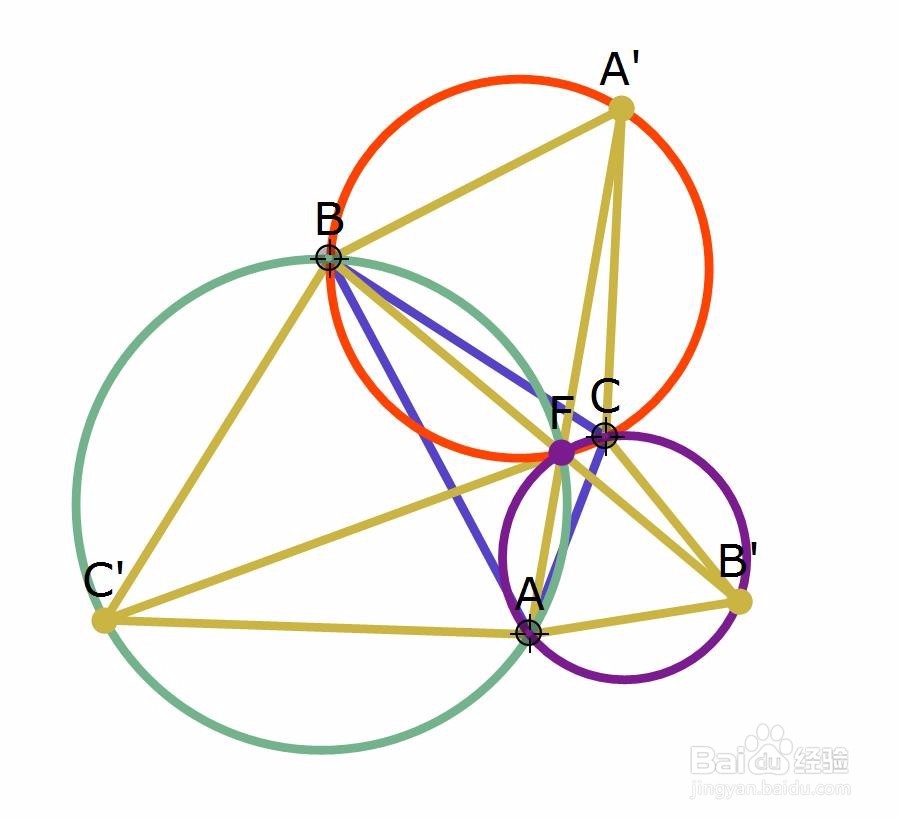
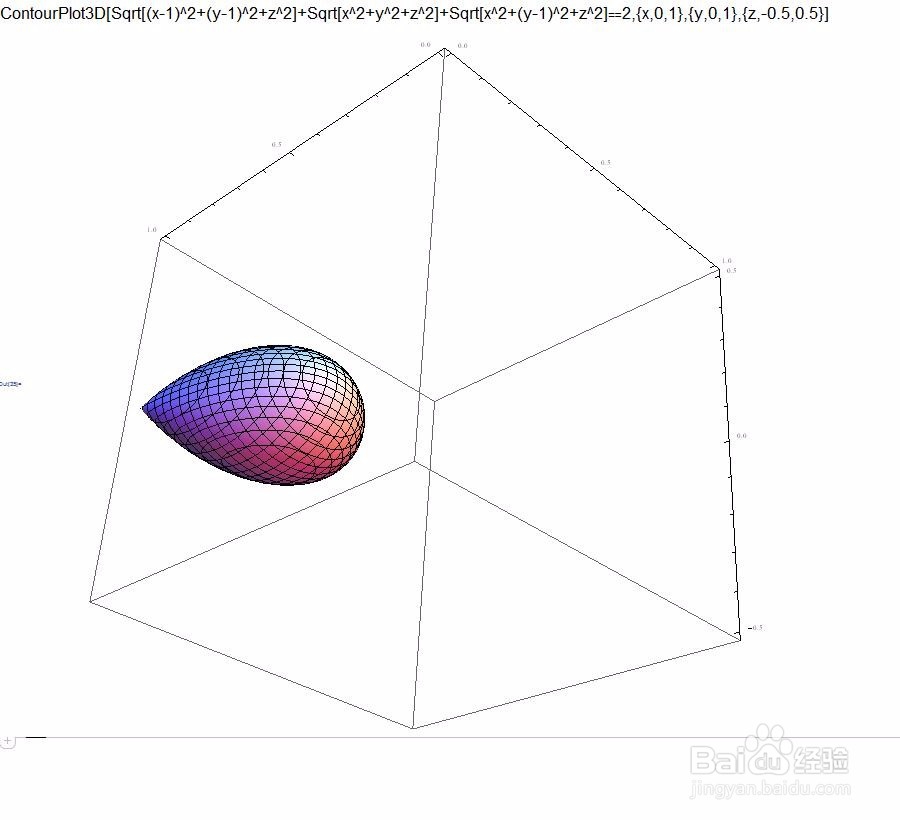
11、状态下的三焦点曲面初探 仍旧以A(0,0,0)、B(0,1,0)、C(1,1,0)为焦点,a=2。 简单的一个代码:ContourPlot3D[Sqrt[(x - 1)^2 + (y - 1)^2 + z^2] + Sqrt[x^2 + y^2 + z^2] + Sqrt[x^2 + (y - 1)^2 + z^2] == 2, {x, 0, 1}, {y, 0, 1}, {z, -0.5, 0.5}] 好像一个水滴。
12、留个问题 用代数方法,求出下式的最小值!