本经验介绍当x^2+y^2=15时,用通过三种方法求x+y和四种方法求xy的取值范围思路即方法步骤。
工具/原料
二次函数相关知识
数学不等式思想
一、求x+y的最值
1、设x+y=k,代入根据二次方程的判别式与根有关性质求得k的取值范围,即得最值。

2、使用三角换元法,代入根据三角函数的有界性性质,求得x+y的最值。

3、利用x与y和的平方和平方和之间不等式关系,求解x+y的取值范围。

二、求xy的最值
1、通过已知条件得到用x来表示y,代入到关于x的一个未知数的代数式,进而根据函数性质求得xy的最值。

2、设xy=p,代入已知条件,并参考使用二次方程判别式与根的关系,求得p即xy的取值范围。

3、使用三角换元法,分别用正弦和余弦来换元x和y,代入所求表达式并根据三角函数的有界性质求得xy的最值。

4、用基本不等式公式a^2+b^2≥2ab,来求解xy乘积的最小值和最大值。

三.结论归纳
1、可见x+y的最值不在已知条件曲线的端点处达到,而是直线y=x与已知条件的交点处达到。其中最大值在第一象限得到,最小值在第三象限得到。
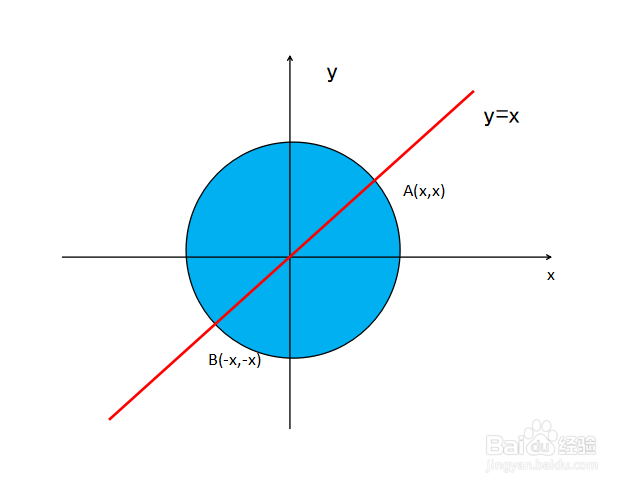
2、 xy的最值也不在已知条件曲线的端点处达到,而是直线y=x,y=-x与已知条件的交点处达到。 其中最大值是y=x在第一象限或第三象限的交点处得到。 其中最小值是y=-x在第二象限或第四象限的交点处得到。