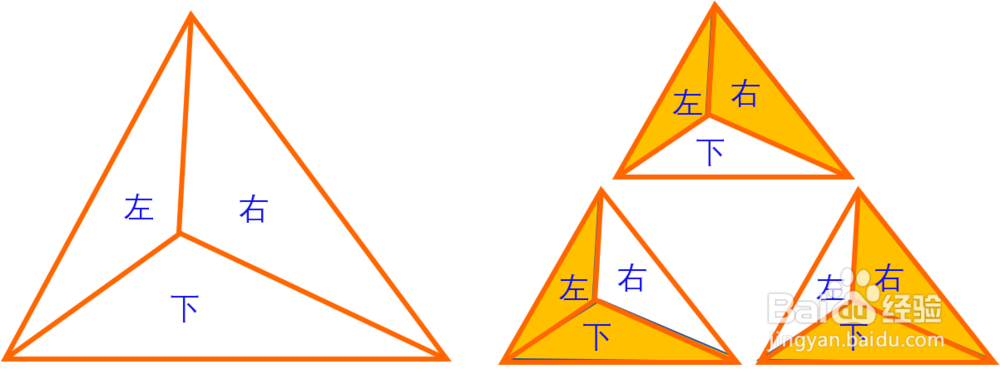
1、燕尾模型研究的是,在一个三角形的内部,某个点与三个顶点分别相连后,所形成得左、右、下三个燕尾三角形,及形成的(左、右)(左、下)(右、下)三组燕尾。但确切的研究,这样的分割还不够完整。
2、下图是从三角形中抽象出来的图形,蓝色部分像燕子的翅膀,绿色部分像燕子的尾巴,在计算三角形面积时,往往需要用到燕尾和翅膀的比例关系。

3、对上面图形勾边,并做标注如下。

4、去掉涂色,并在内部添加线段,如下图。这就是燕尾模型最常见的形状。由此,我们可以得到线段与三角形面积之间的关系:1)翅膀之比等于尾巴之比SΔABG: SΔACG= SΔBGE: SΔCGE =BE:CESΔBGA: SΔBGC= SΔGAF: SΔGCF =AF:CFSΔAGC: SΔBGC= SΔAGD: SΔBGD =AD:BD2)翅膀面积之和:尾巴面积=翅骨:尾骨SΔABG+ SΔACG): SΔBGC=AG:GE3)线段之间的比值:(BE÷CE)×(CF÷AF)×(AD÷BD)=1

5、经典案例:如图E在AD上,AD⊥BC,AD=300px,DE=75px,求SΔABC是SΔEBC的几倍?

6、根据燕尾定理模型,S翅膀:S尾巴=AE:EDSΔABC= S翅膀+S尾巴SΔEBC= S尾巴SΔEBC÷ SΔEBC= 12÷3=4
7、小学数学几何部分的学习,要注重分类总结,并把知识点模型化。如果掌握了以上基础模型,那么学习就会事半功倍。