1、我们碍测行臬试图用Mathematica找到这两条曲线的交点。sol=Solve[1+Cos[2 t]==1+Sin[t]&&0<t<2*Pi](*加以验证*){1+Cos[2 t],1+Sin[t]}/.sol

2、分析一下:要绘制公共部分,那么在 -7 Pi/瀵鸦铙邮6<t<Pi/6 的时候,保留 1+Sin[t] ;在 Pi/6<t<5 Pi/6 的时候,保留 1+Cos[2 t] ,这实际上是一个分段函数:PolarPlot[ Piecewise[{{1+Sin[t],-7 Pi/6<=t<Pi/6}, {1+Cos[2 t],Pi/6<=t<=5*Pi/6}}], {t,-7*Pi/6,5 Pi/6},PlotRange->{{-2,2},{-1,2}}]
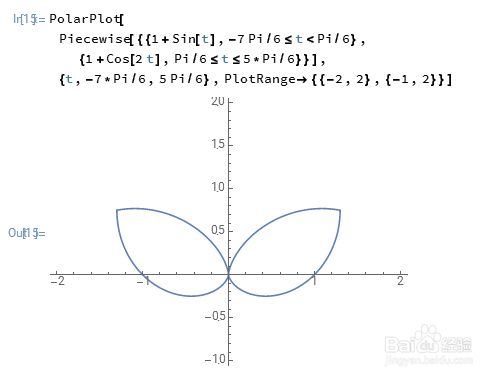
3、这个分段函数还可以用If来构造:If[-7 Pi/6<=t<Pi/6,1+Sin[t],1+Cos[2 t]]得到的结果是一样的。
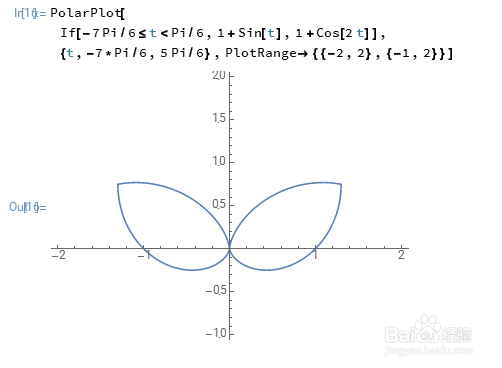
4、用网络画板画这个图,可以使用if函数(反正构造出分段函数就行了):ρ=if(-7 * pi / 6 <= thet and thet < pi / 6, 1 + sin(thet), 1 + cos(2 * thet))

5、后来,一个大牛给出了一个精彩的方法,可以很容易的解决这一类问题:PolarPlot[Min[1+Sin[t],1+Cos[2 t]],{t,0,2 Pi}, PlotRange->{{-2,2},{-1,2}}]
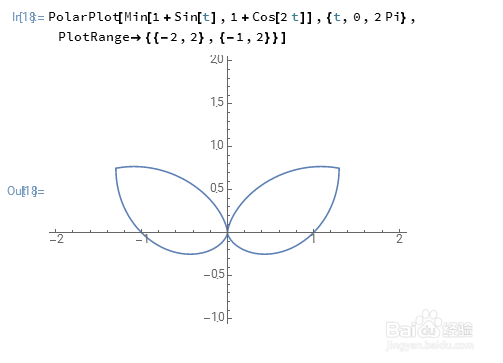
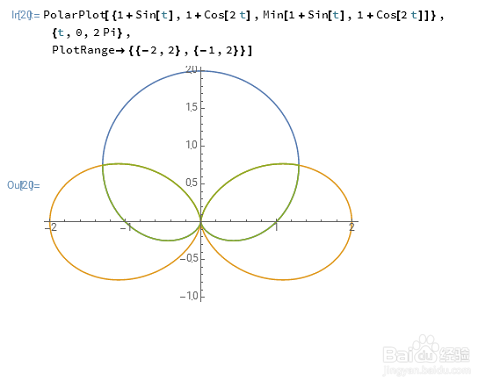
6、这个方法也可以借鉴到网络画板里面:ρ=min(1 + sin(thet), 1 + cos(2 * thet))

7、用Min(Mathematica)或min(网络画板 ),就可以很方便的把多个极坐标曲线的公共部分构造出来:PolarPlot[{Sin[2 t],Sin[t],Sin[3 t柯计瓤绘]},{t,0,2 Pi}]PolarPlot[Min[Sin[2 t],Sin[t],Sin[3 t]],{t,0,2 Pi}]和ρ=min(sin(3 * thet), sin(thet), sin(2 * thet))这个好像不是公共区域吧!因为三个图形都是关于y轴对称的,而公共部分却不是。你们知道怎么回事吗?


