1、求解一阶导数的公式:y'=[y猾诮沓靥(x0+h)-y(x0-h)]/(2h);求解二阶导数的公式:y''=[y(x0+h)-2*y(x0)+y(x0-h)]/h罡蛑噬唔²;这里的自变量是x,因变量是y,步长是h
2、再进行编程。以下是我的求解程序:clc;clear allh=0.01;%x属于【a,b】a屏顿幂垂=-5;b=5;x=a:h:b;荏鱿胫协n=length(x);%定义yy=sin(0.3*x).*cos(3*x);hold ongrid onyx=zeros(1,n);yxx=zeros(1,n);for i=2:n-1 yx(i-1)=(y(i+1)-y(i-1))/(2*h); yxx(i-1)=(y(i+1)+y(i-1)-2*y(i))/h^2;endplot(x,y,'r','linewidth',2)plot(x(2:n-1),yx(1:n-2),'g','linewidth',2);plot(x(2:n-1),yxx(1:n-2),'b','linewidth',2);legend('原函数','差分一阶导数','差分二阶导数')xlabel('$$x$$','Interpreter','latex','color','r','fontsize',28);ylabel('$$y$$','Interpreter','latex','color','r','fontsize',28);
3、复制以上程序到*.m文件中去,保存并运行,可以得到函数图像确实十分接近理论上的解答。以下是运行以后作出的图。
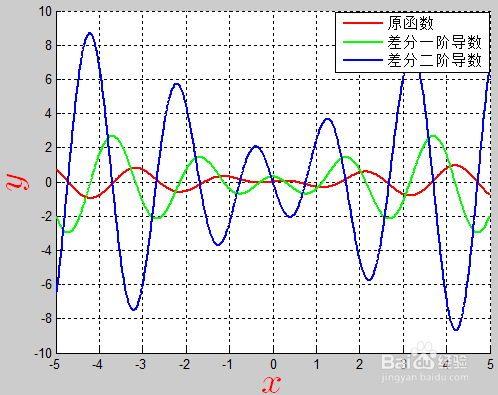
4、最后就大功告成啦!对于任意一组数据(间距相等)这个程序都可以很好滴求解一阶导数、二阶导数哟;还有你可以加以改进,不管是间距相等还是不相等都好做。