本文,介绍一下Mathematica对多项式的简单处理方法。

工具/原料
电脑
Mathematica
不分主次的介绍
1、PolynomialRemainder[x^2, x + y^3, x]计算x^2除以x + y^3得到的余式。Remainder——剩余。

2、PolynomialQuotient[x^2, x + y^3, x]计算x^2除以x + y^3得到的商式。Quotient——商,商数。

3、PolynomialMod[x^2, x + y^3]这个函数的作用,类似于求余数。但是,有的时候,PolynomialMod和PolynomialRemainder 的结果有可能不相同。


4、用PolynomialGCD求下面两个多项式的公因式:x^3-2x^2+2x-1;x^5+x^4+2x^3+9x^2-3x-10。

5、用PolynomialLCM求这两个多项式的最小公倍式,也就是多项式的乘积除以最大公因式。

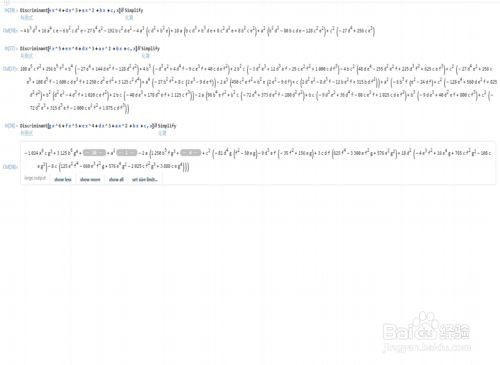
6、用Discriminant计算多项式的判别式,但是一元六次方程的判别式已经复杂到难以显示了。

7、已知几个二维空间的点的坐标——{a,b}, {c,d}, {e,f},用InterpolatingPolynomial求出对应的插值多项式。
