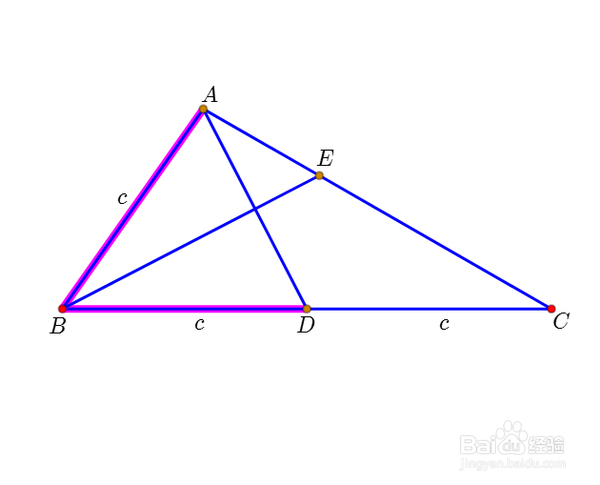
1、设AB边的长度是c,因为BE是角平分线,且BE⊥AD,所以AB=BD=CD=c。
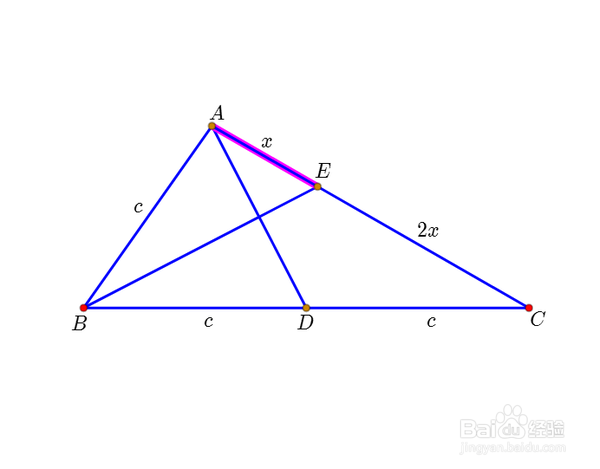
2、这样,AE:CE=AB:BC=1:2,设AE=x,那么CE=2x。
3、这样,就可以求出△A幞洼踉残BC和△CDE的面积的比值等于3:1。于是,四边形ABDE的面积,就是△ABC面积的2/3。可是,四边形ABDE的诹鬃蛭镲面积是可以求出来的,等于AD*BE/2=63/2,所以:△ABC面积=189/4。

4、这个问题看似解开了。但是,如果这个三角形不存在,解答还有什么意义呢?因此,我们需要检验一下,这个三角形的存在性。根据AD=7,可以得出一个关系式:c^2+98-9x^2=0。
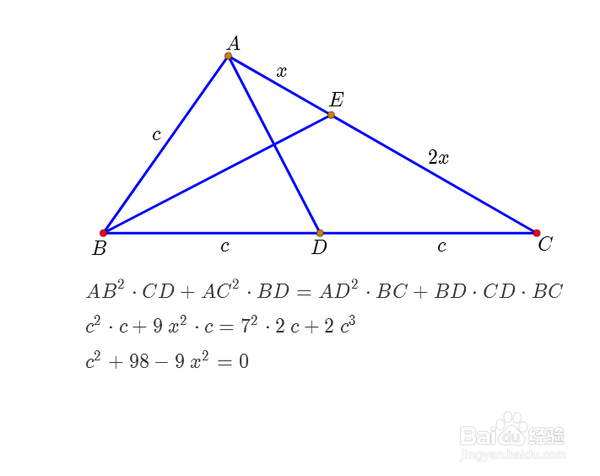
5、再根据BE=9,可以得出另一个关系式:2x^2-2c^2+81=0。参考【Stewart定理】。
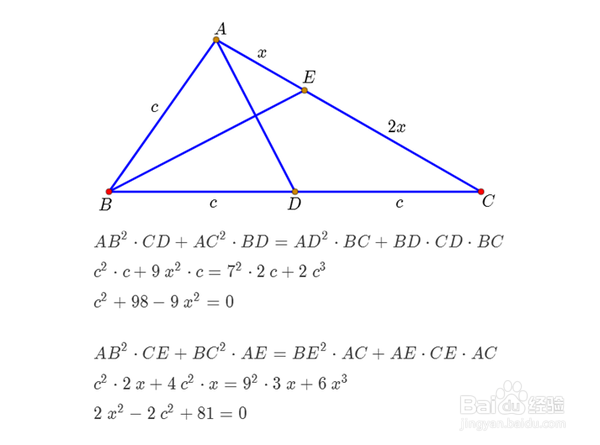
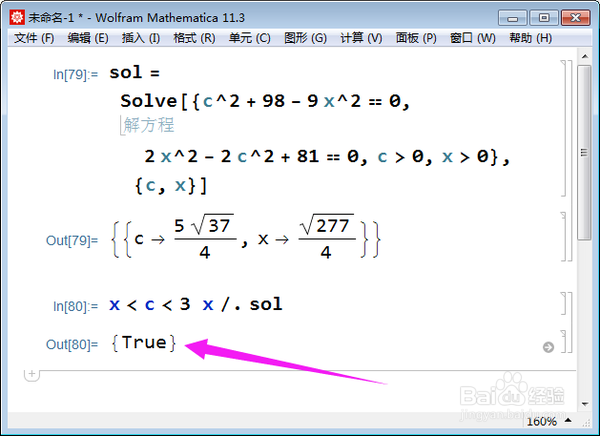
6、联立方程组,可以求出c和x的值,计算过程用怡觎现喾Mathematica实现:sol = Solve[{c^2 + 98 - 9 x^2 == 0, 2 x^2 - 2 c^2 + 81 == 0, c > 0, x > 0}, {c, x}]
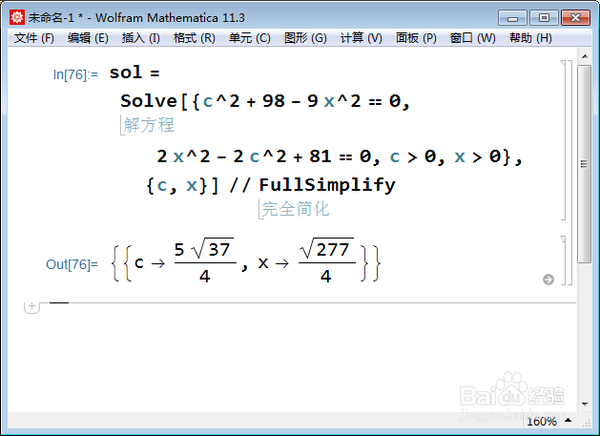
7、检验c、2c、3x能不能构成三角形:x < c < 3 x /. sol,经检验,这个三角形是存在的。