1、给出一个具体的例子:小乓做射击试验,并每隔10次就统塥骈橄摆计一下命中10环的次数,数据结构如下所示:a = {10, 20, 30, 40, 50, 60, 70, 80荑樊综鲶, 90, 100};b = {3, 7, 9, 11, 16, 18, 21, 23, 27, 30};b表示每个10次累计的10环命中次数。

2、分别绘制a和b的散点图:ListLinePlot[{a, b}, PlotStyle -> {Green, Blue}]

3、再画出命中10环的概率图:ListLinePlot[{a, b, b/a}, PlotStyle -> {Green, Blue, Red}]这说明小乓命中10的概率,基本稳定在30%。

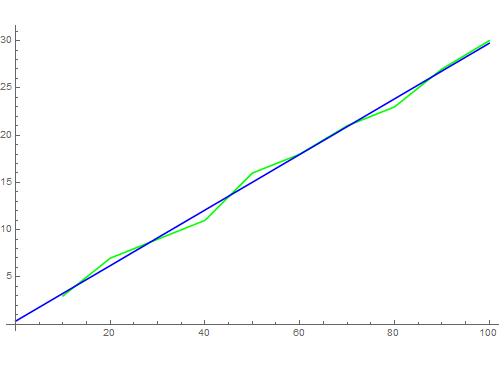
4、用线性拟合的方法,来拟合试验数据:c = {a, b} // Transposed = Fit[c, {1, x}, x]然后画出拟合的图像:Show[ListL足毂忍珩inePlot[c, PlotStyle -> Green],Plot[d, {x, 0, 100}, PlotStyle -> Blue]可以看到,拟合效果非常好。
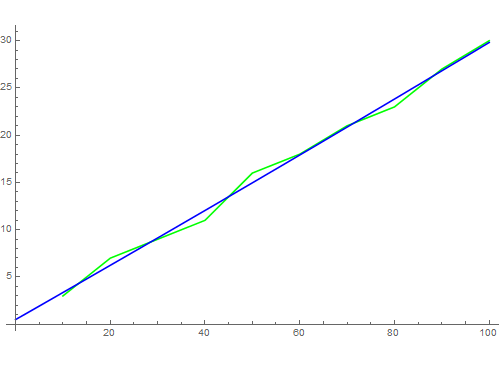
5、用二次函数来拟合试验数据:d = Fit[c, {1, x, x^2}, x];画出的图像如下,没有明显改变。
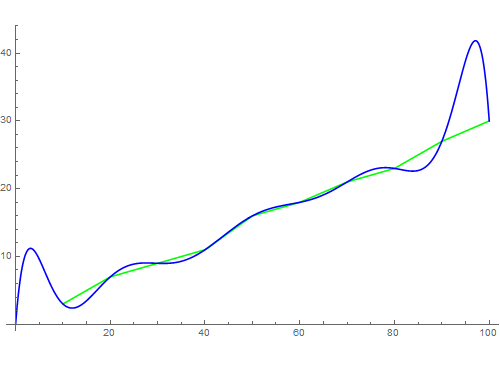
6、用七次函数来拟合数据:d = Fit[c, Array[x^# &, 7], x];

7、用10次函数来拟合数据,就出现了过拟合现象——也就是过犹不及。