微分和增量存在以下关卺肿蓦艚系:
微分在数学中的定义:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函剞麽苍足数在dx处的微分,微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。微积分的基本概念之一。
增量则是指在某一段时间内系统中保有数量的变化。这三者之间的关系可用以下两个公式表示:增量=流入量-流出量;本期期末存量=上期期末存量+本期内增量。
增量是指数的变化值,即数值的变化方式和程度。增量本身也是一个数。数的变化有增加和减少两种情况。当数增加时,增量为正;当数减少时,增量为负。
增加或减少的越多,增量的绝对值就越大。如3增大到5,则3的增量为+2;3减少到1,则3的增量为-2。换句话说,增量就是变化后的数值与原数值的差。
增量是这点的函数自变量X增加△X,Y增加△Y.△Z=f(X1+△X,Y1+△Y)-f(X1,Y1)
且对△Z取极限等于0.那么△Z就是函数Z=f(X,Y)在点(X1,Y1)处的全增量。
也就是X,Y同时获得增量.而全微分是先对X求导,所得乘d(X),在对Y求导,所得乘d(Y),再把两个先加就是微分。
扩展资料
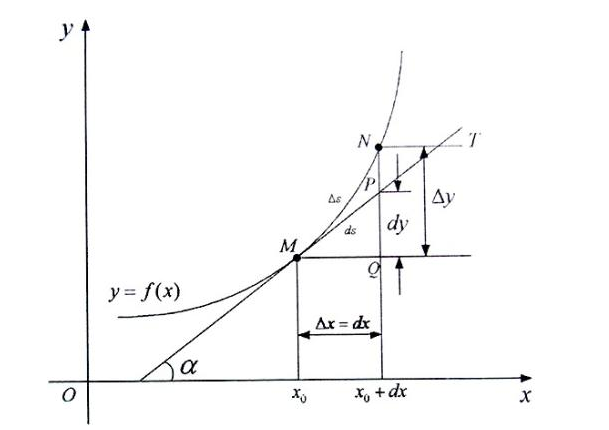
微分当自变量为固定值需要求出曲线上一点的斜率时,前人往往采用作图法,将该点的切线画出,以切线的斜率作为该点的斜率。然而,画出来的切线是有误差的,也就是说,以作图法得到的斜率并不是完全准确的斜率。
以y=x2为例,我们需要求出该曲线在(3,9)上的斜率,当△x与△y的值越接近于0,过这两点直线的斜率就越接近所求的斜率m,当△x与△y的值变得无限接近于0时,直线的斜率就是点的斜率。
参考资料来源:百度百科-微分