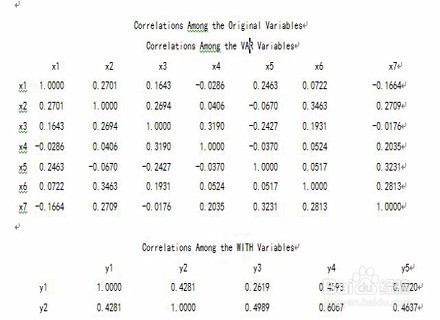
1、对x8、x12进行正向化,给出相关系数阵R11(Correlations Among the VAR Variables)、R12(Correlations Between the VAR Va根据riables and the WITH Variables)、R22(Correlations Among the WITH Variables);教科书P258例1的数据可以发现,X1~X 7、X9~X 11是正变量,x8、x12为逆向量,因此跑步秒数是越短越好。因此我们把X8按公式x8=50/X8进行正向化,正向化后意义成为: 50米跑的速度(m/s),具有正向的意义。X12按公式x12=1500/X12进行正向化,正向化后意义成为: 1500米跑的速度(m/s)具有正向的意义,与原变量反映的实际意义相同。

2、同时根据SAS程序得出对应的相关矩阵,R11(Correlations Among the VAR Variables)、R12(Correlations Between the VAR Va根据riables and the WITH Variables)、R22(Correlations Among the WITH Variables)得出表
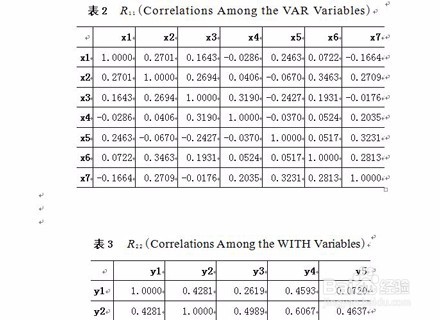
3、给出典型相关系数(Canonical Correlation)、标准化典型变量函数(Standardized Canonical Coefficients for the VAR Variables、Standard- ized Canonical Coefficients for the WITH Variables)。给定显著水平=0.01,通过查相关系数表得出=0.413其中典型相关系数1=0.8521,2=0.6976,3=0.6447都是大于=0.413,因此可以得出1、2、3都是高度显著的,可以用于进行典型分析,而4、5都是小于=0.413,因此可以得出4、5都对变量价值贡献不大,不用用于做典型分析。

4、通过x1-x7与典型变量Ui(i=1、…、5)的相关系数(Correlations Betw- een the VAR Variables and Their Canonical Variables),选出与典型变量Ui显著相关的变量,对Ui命名及其正向化;通过x8-x12与典型变量Vi的相关系数(Correlations Between the WITH Variables and Their Canonical Variables),选出与典型变量Vi显著相关的变量,对Vi命名及其正向化。给出Ui、Vi中选出变量的相关性影响分析; 根据上述数据:可以得知前三个变量值得于分析。选择系数绝对值大于=0.413的值进行分析

5、我们对给出的Ui、Vi中选出变量的相关性影响分析:根据已有数据,我们知道对原始变量的研究可以化为前三个变量的影响研究分析,从相关性了解两种原始变量的关系。同时我们事先对逆向量进行正向化,因此数据越大,影响越好。第一对典型变量中,U1里面中做好x1~x3以及V1中x8~ x12的提升就能促进运动能力测试各项指标的提高,提升运动能力测试水平。第二对典型变量中,U2中可以保持台阶试验(指数)的影响,协调发展纵跳(cm)的能力发展,在V2中可以知道在跳远中,腿部的能力,显示出跳远的能力的情况。 第三对典型变量中,协调提高x7(俯卧上体后仰(cm))、x2(纵跳(cm))的能力,进而提升俯卧上体后仰与纵跳的能力的影响。再能够进一步短跑与耐力跑的影响产生促进的作用。

6、实验程序部分如下:data fit; input x1-x7 鲻戟缒男y1-y5; cards;46.00 55.00 126.00 51.00 75.00 25.00 72.00 7.35 489.00 27.00 8.00 4.1752.00 55.00 95.00 42.00 81.20 18.00 50.00 6.94 464.00 30.00 5.00 4.3146.00 69.00 107.00 38.00 98.00 18.00 74.00 7.35 430.00 32.00 9.00 3.89run;proc cancorr data=fit simple corr vprefix=u wprefix=v; var x1-x7; with y1-y5;run;