1、根据素数的定义,写一个粗略的自定义函数:def p(n): if str(n).isdigit() and n>1: for i in range(2,n-1): if n%i==0: return False return True else: print('变量有误,请输入大于1的整数。')

2、先检验一下这个函数是否靠谱:for i in range(36): print(i,' ',p(i))看来还是挺靠谱的。

3、我们查看一下,用这个函数检测8000以内的所有素数,需要用多长时间:import timea=time.clock()for i in range(2,8000): p(i)b=time.clock()print('用时%s秒。'%(b-a))

4、前30000个素数的判别,用时为2秒多点。

5、用这个函数判断2^100+45是否素数,用时长达36秒:import timea=time.clock()i=2**100+45p(i)b=time.clock()print('用时%s秒。'%(b-a))
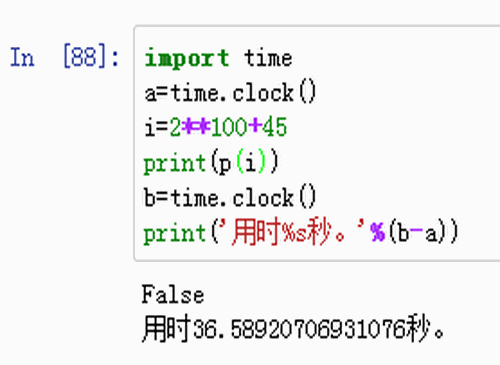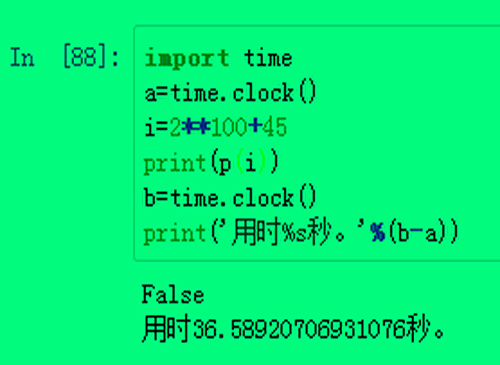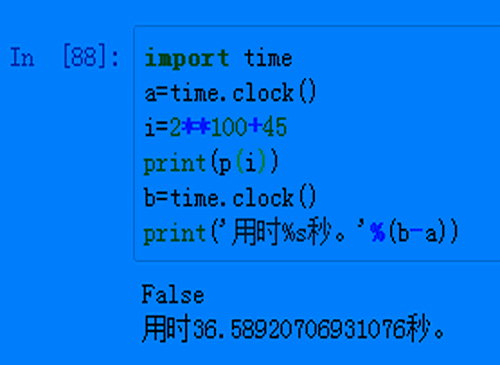
6、我们来写出2^100+45最小的素因子,就得先修改自定义函数:def p(n): if str(n).isdigit() and n>1: for i in range(2,n-1): if n%i==0: print(i) return False return True else: print(n,'变量有误,请输入大于1的整数。')然后开始检测:import timea=time.clock()i=2**100+45print(p(i))b=time.clock()print('用时%s秒。'%(b-a))


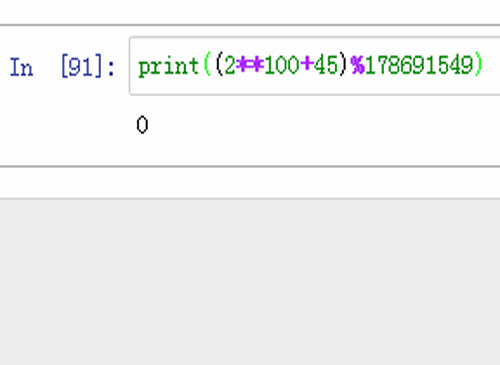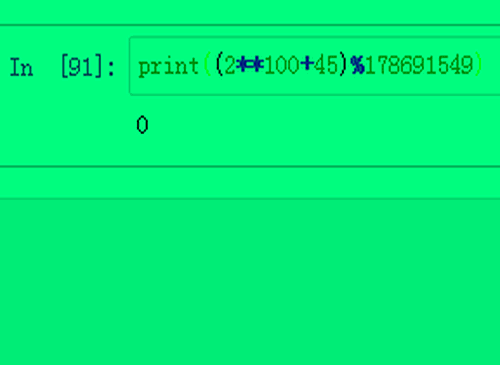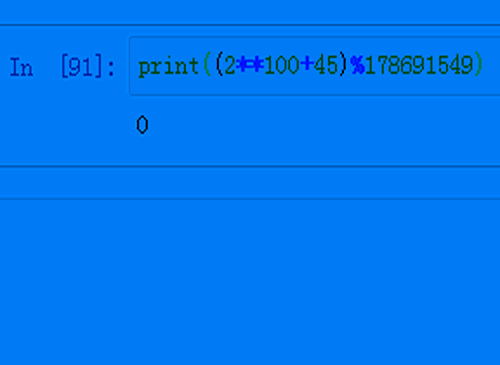
7、再检验一下:print((2**100+45)%178691549)运行结果等于0,说明2^100+45确实不是素数。