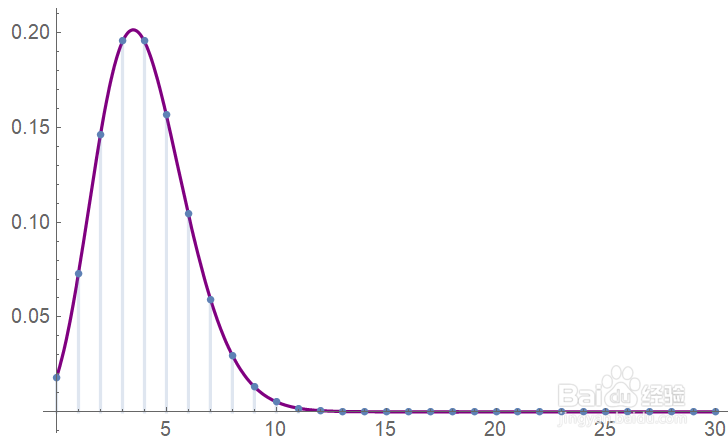
1、在Mathematica中,二项分布的符号是BinomialDistribution[n,p]二项分布相当于n次独立的概率为p的两点分布结果的和的分布。其概率函数如图。

2、Binomial[n,x]则是计算二项系数(n个里取x个的情况数),即n!/(x!(n-x)!)如图计算了二项式系数前四项。

3、二项系数和二项式以及以及杨辉三角联系密切。如图代码显示一个杨辉三角。

4、下面,我们使用DiscretePlot函数绘制二项分布B(n,0.5)的分布。n分别取10,30,50,70.可以看到,n越高,分布越平滑,同时平均值增大。
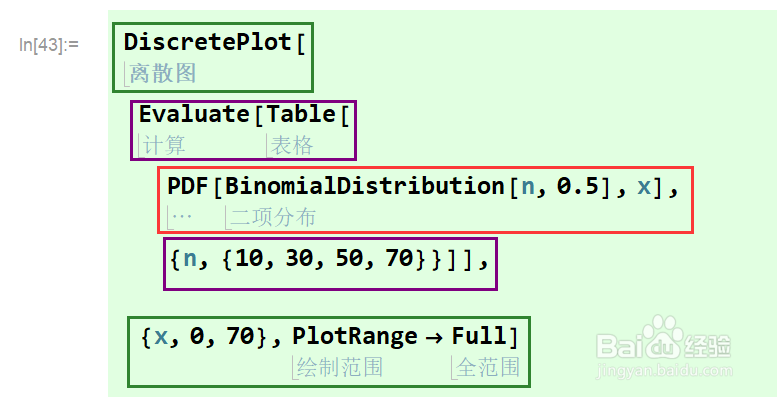

5、注意:当我们使用二项分布和二项系数时,不要把Binomial写成Binomal,后者是二元正态分布。是Bi(二元)+normal(正态),而不是Binomial。

6、二项分布B(n,p)的平均值为np,方差为n(1-p)p。方差有时也记作npq,p是每一次两点分布为1的概率,q是为0的概率即1-p.

7、当我们计算(X-n*p)的分布时(X是二项分布B(n,p)),当p不变,n增大时,二项分布逼近正态分布的样子。(准确的说,变换若取(X-n*p)/Var(X)会趋近于标准正态分布,但是在离散概率下不方便变换和画图)

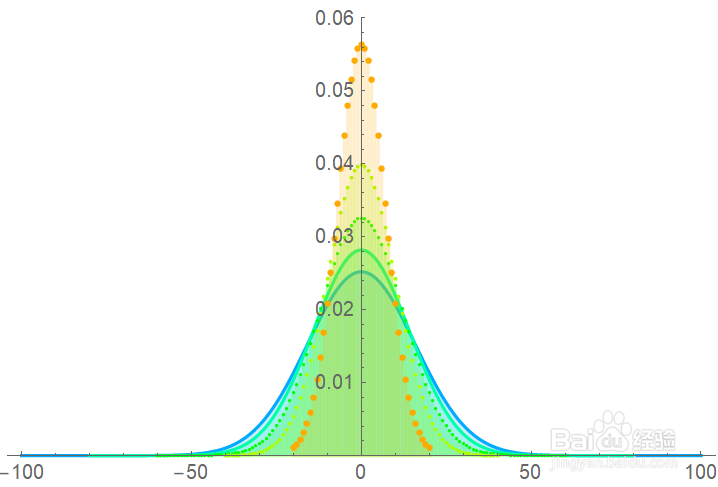
8、当λ=np为定值时,随着n的增大,p变小,这样的二项分布趋近于泊松分布。效果如图。实线是泊松分布。