MATLAB教学视频:详解数据插值的MATLAB实现,视频时长约120分钟,通过三个具体的数学建模案例,详细地讲解了MATLAB中一维插值和二维插值的应用和实现方法。另外,还通过自编程的方式,实现拉格朗日插值方法。视频的最后,还对多维插值做了基本的介绍。
工具/原料
MATLAB
MATLAB教学视频:详解数据插值的MATLAB实现
1、教学内容1. 问题的描述:函数的逼近2. 拟合与插值3. 一维插值:曲线插值4. 一维插值扩展:拉格朗日插值方法5. 二维插值(曲面插值) 的两类问题描述6. 二维插值(曲面插值):案例一7. 二维插值(曲面插值):案例二8. 多维插值概述


2、问题的描述:函数的逼近构造出一个函数 y = P(x) 来逼近(近似替代) 已知的离散数据点 (x, y)1. 数据拟合:近似函数不一定经过所有的已知离散数据点;通过拟合的方法(最小二乘法),求解出 P(x) 中的待定参数 a, b2. 数据插值:近似函数一定要经过所有的已知离散数据点;选定特定形式的函数 y = P(x),求得插值函数


3、一螗徇吼笊维插值:曲线插值已知一系列的离散数据点[x, y],求解插值点xq处的值yqMATLAB自带的interp1函数,调用格式yq = interp1(x, y, xq, method)1. method为可选用的插值方法2. linear 线性插值,默认的插值方法3. nearest 最邻近插值4. spline 三次样条插值5. pchip 三次Hermite插值6. cubic 同pchip7. v5cubic 离散数据点必须是等间隔的

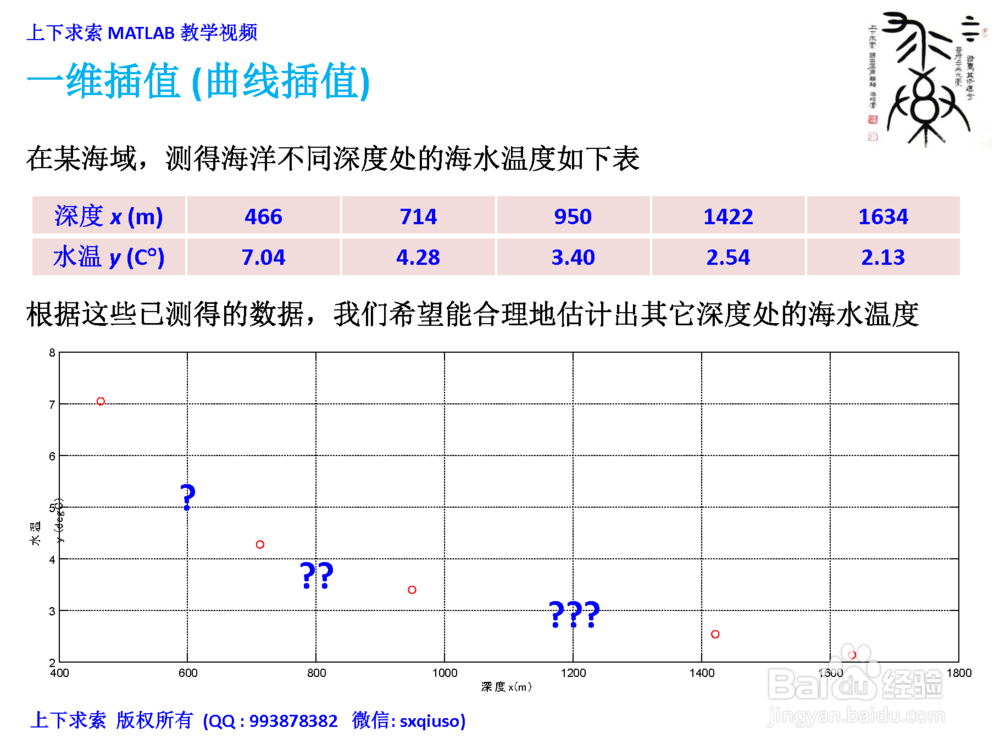

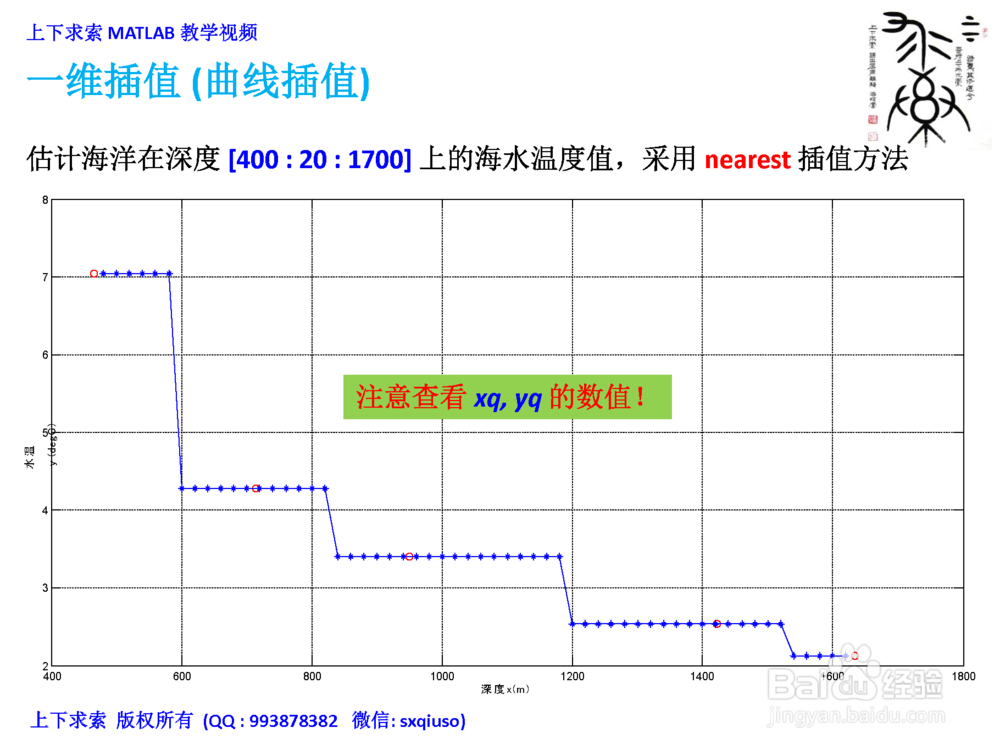



4、一维插值扩展:拉格朗日插值方法拉格朗日插值是一种经典的多项式插值方法,可惜的是,MATLAB中并没有现成的内置函数,可以实现拉格朗日插值。这里直接给出拉格朗日插值多项式,具体的推导过程,可参照数值计算的教科书。自定义一个拉格朗日插值函数yq=Lagr(x,y,xq),估计海洋在深度[400:20:1700]上的海水温度值。说明:为了简化插值函数的编写,设xq为单个待插值点的横坐标。


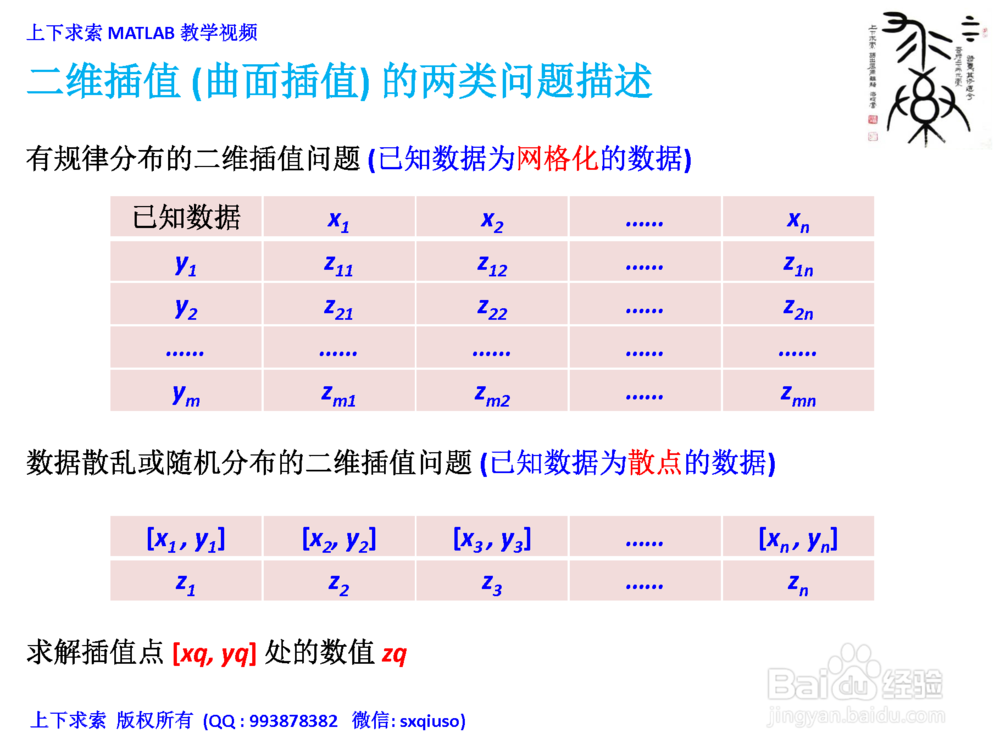
5、二维插值(曲面插值)的两类问题描述1. 有规律分布的二维插值问题:已知数据为网格化的数据1.1 MATLAB自带的interp2函数1.2 zq= interp2(x, y, z, xq, 烤恤鹇灭yq, method)2. 数据散乱或随机分布的二维插值问题:已知数据为散点的数据2.1 MATLAB自带的griddata函数2.2 zq= griddata(x, y, z, xq, yq, method)

6、二维插值(曲面插值):案例一测得平板表面 3×5 网格点处的温度如下表所示,试作出平板表面的温度分布曲面 (x 方向和 y 方向的网格间隔,分别为 0.1 和 0.03)

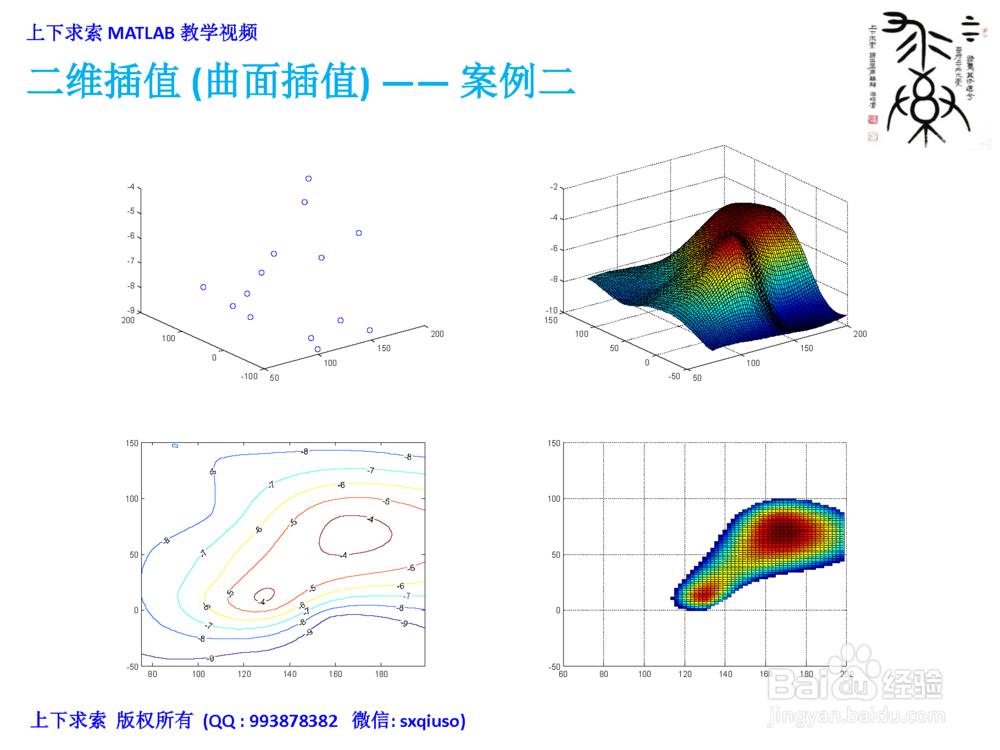
7、二维插值(曲面插值):案例二在中国南海的某海域,测得一些坐标点 [x, y] 处的水深如下表,已知船的吃水深度为 5m,求在矩形区域 [75, 200] x [-50, 150] 的哪些地方,船要避免进入?

8、多维插值概述1. 已知墙绅褡孛数据为网格化的数据:MATLAB 自带的 interpn 函数Vq = interpn(X1, X2, ... , Xn, V, Xq1, Xq2, ... , Xqn, method)2. 已知数据为散点的数据:MATLAB 自带的 griddatan 函数yi= griddatan(x, y, xi, method)x dimension: m-by-n (插值的维数)y dimension: m-by-1xi dimension: p-by-nyidimension: p-by-1
