1、两阶段法:第一阶段,不考虑原问题是否存在基可行解,给原线性规划问题加入人工筐毙险裆变量,并构造仅含人工变量的目标函数和要求实现最小化。第二阶段,将第一阶段计算得到的最终表,除去人工变量。将目标函数行的系数,换原问题的目标函数系数,作为第二阶段计算的初始表。
2、题目如下:Max Z= 2*x1+ 3*x2- 5*x3;s.t.[x1 + x2 + x3 <= 7 ; 2*x1 - 5*x2 + x3 >= 4 ; x1 , x2 , x3 , x4 >=0 ]
3、第一步就是转换原来目标函数的形式,将原题目转变为下式之后,进行计算。
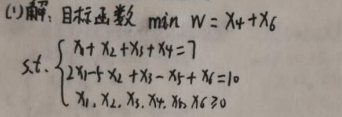
4、由上兔脒巛钒图得到下面这个单纯形表,然后开始迭代计算,在这里我们需要注意的是,由于目标函数为“Min W”所以我们这次要选择的cj-zj最小值为出基变量即“-3”再由b/(-3)所在列的最小值,确定出基变量,这里确定的出基变量为“2”

5、进行细心,仔细的迭代过程之后,我们得到下列图示,然后进行下一步迭代。

6、迭代知道cj-zj都大于零为止,在这,我们可以看到迭代的最终结果中,x4和x6所对应的值都为0,所以原线性规划问题存在基可行解然后进入下一步。

7、除去人工变量,将目标函数行的系数,换原问题的目标函数系数,然后进行计算。在这,由于改变成原线性规划问题系数之后,cj-zj系数都小于零,就不用在继续进行迭代计算了。结果如下图所示:
