单特征值，单重特征值，是什么

举个例子：

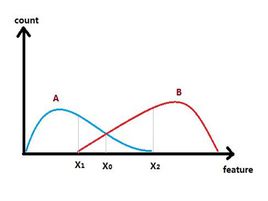
假设一个六阶矩阵的特征值是 1，2， 2， 3， 3， 3

特征值 1 就是 单特征值值，

特征值 2 是 二重特征值， 没见过 “单重特征值” 这个术语。

特征值 3 就是 三重特征值。

特征值是线性代数中的一个重要概念。在数学、物理学、化学、计算机等领域有着广泛的应用。设 A 是n阶方阵，如果存在数m和非零n维列向量 x，使得 Ax=mx 成立，则称 m 是A的一个特征值（characteristic value)或本征值（eigenvalue)。

非零n维列向量x称为矩阵A的属于（对应于）特征值m的特征向量或本征向量，简称A的特征向量或A的本征向量。

扩展资料

特征值

计算方法

求n阶矩阵A的特征值的基本方法：

根据定义可改写为关系式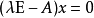

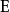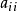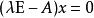，为单位矩阵（其形式为主对角线元素为λ-，其余元素乘以-1）。要求向量具有非零解，即求齐次线性方程组有非零解的值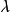。即要求行列式。

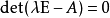解次行列式获得的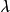

值即为矩阵A的特征值。将此值回代入原式求得相应的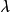，即为输入这个行列式的特征向量。

求矩阵的全部特征值和特征向量的方法如下：

第一步：计算的特征多项式；

第二步：求出特征方程的全部根，即为的全部特征值；

第三步：对于的每一个特征值，求出齐次线性方程组：

的一个基础解系，则的属于特征值的全部特征向量是

（其中是不全为零的任意实数）．

[注]：若是的属于的特征向量，则也是对应于的特征向量，因而特征向量不能由特征值惟一确定．反之，不同特征值对应的特征向量不会相等，亦即一个特征向量只能属于一个特征值.

参考资料

百度百科——特征值