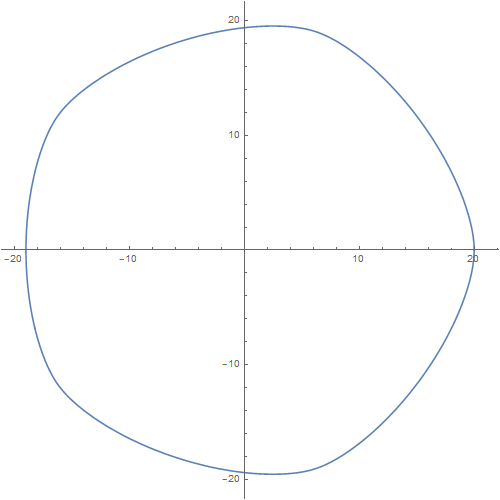
1、等宽曲线一定是凸曲线;而光滑的等宽曲线,上面的每一个点的切线,就是相应位置的支持线。如果给出某条凸曲线的支持函数:f缪梨痤刻[t_] := 2 Cos[3 t/2]^2 + 8我们就可以画出这条凸曲线:ParametricPlot[{f[t] Cos[t] - f'[t] Sin[t],f[t] Sin[t] + f'[t] Cos[t]}, {t, 0, 2 Pi}]
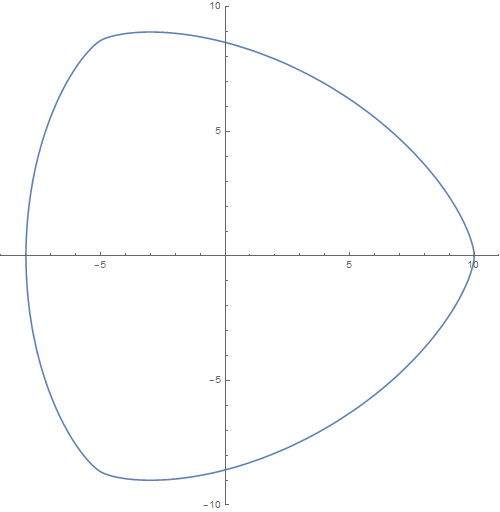
2、x[t_] := f[t] Cos[t] - f&拭貉强跳#39;[t] Sin[t]y[t_] := f[t] Sin[t] + f'[t] Cos[t]我们需要证明唁昼囫缍这是一条光滑的等宽曲线。光滑的意思就是,切线的方向是连续变化的,这条曲线显然满足要求。再证明这是凸曲线,先求出曲线在任意点的相对曲率:(x'[t]*y''[t] - x''[t] y'[t])/(x'[t]^2 + y'[t]^2)^(3/2)由此可知,无论t取什么实数,相对曲率都不会变号,因此,这是凸曲线。

3、再证明,在参数等于t、t+Pi的两条切线是平行的。也就是证明,y'[t]*x'[t + Pi] - y'[t + Pi]*x'[t]等于0:y'[t]*x'[t + Pi] - y'[t + Pi]*x'[t] // FullSimplify

4、最后,证明等宽。Total[({x[t], y[t]} - {x[t + Pi], y[t + Pi]})^2] //FullSimplify // Sqrt从而,我们证明了这是一条处处光滑的等宽曲线。

5、再换一个例子试试:f[t_] := 2 Cos[5 t/2]^2 + 8但是,这不是一条等宽曲线,甚至不是一条凸曲线。可是为什么代数判断都符合呢?这里需要特别注意,要通过相对曲率来判断某条闭合曲线是不是凸曲线,先得保证这条曲线是简单曲线,没有自交点。

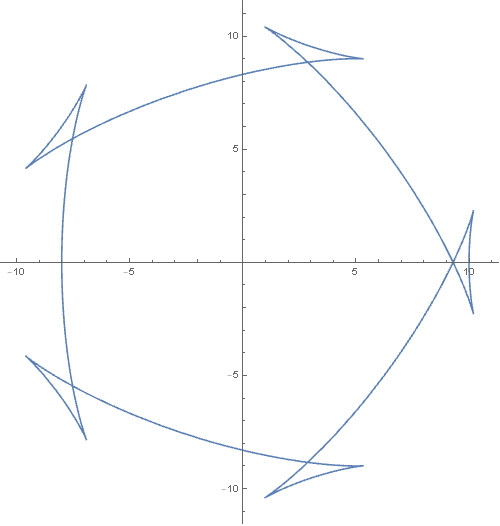
6、再试试这条曲线:f[t_] := Cos[5 t/2]^2 + 19