1、大多数多项式适用的积分公式。比如多项式:y = a*x^n.

2、系数除以(n+1),然后指数加上1。换句话说y = a*x^n 的积分是y = (a/n+1)*x^(n+1).
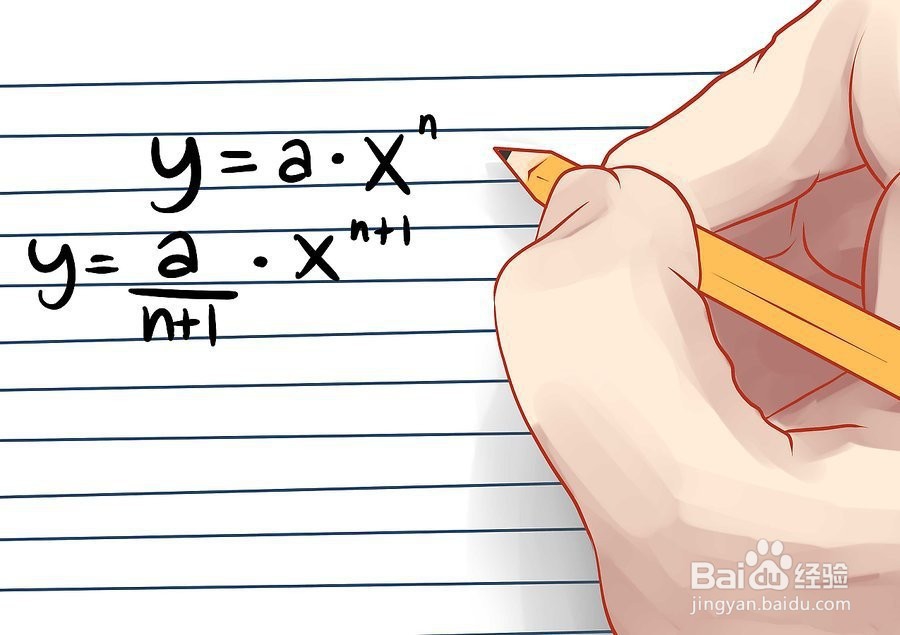
3、对于不定积分,一个多项式对应多个,所以要加上积分常数觊皱筠桡C。因此本例的最终结果是y = (a/n+1)*x^(n+1) + C。考虑这样一个维咩缡朊问题:在计算微分是,所有常数项都被省略。因此,在求积分时,积分结果可以加上任意的常数。
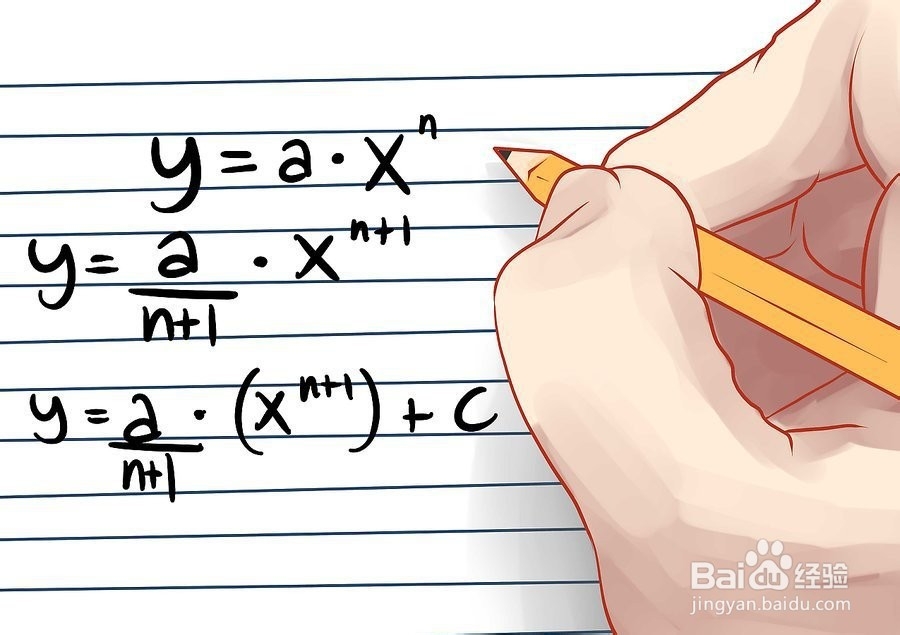
4、根据这个公式,计算积分。比如,y = 4x^3 + 5x^2 +3x的积分是(4/4拘七呷憎)x^4 + (5/3)*x^3 + (3/2)*x^2 + C =x^4 + (5/3)*x^泌驾台佐3 + (3/2)*x^2 + C.
