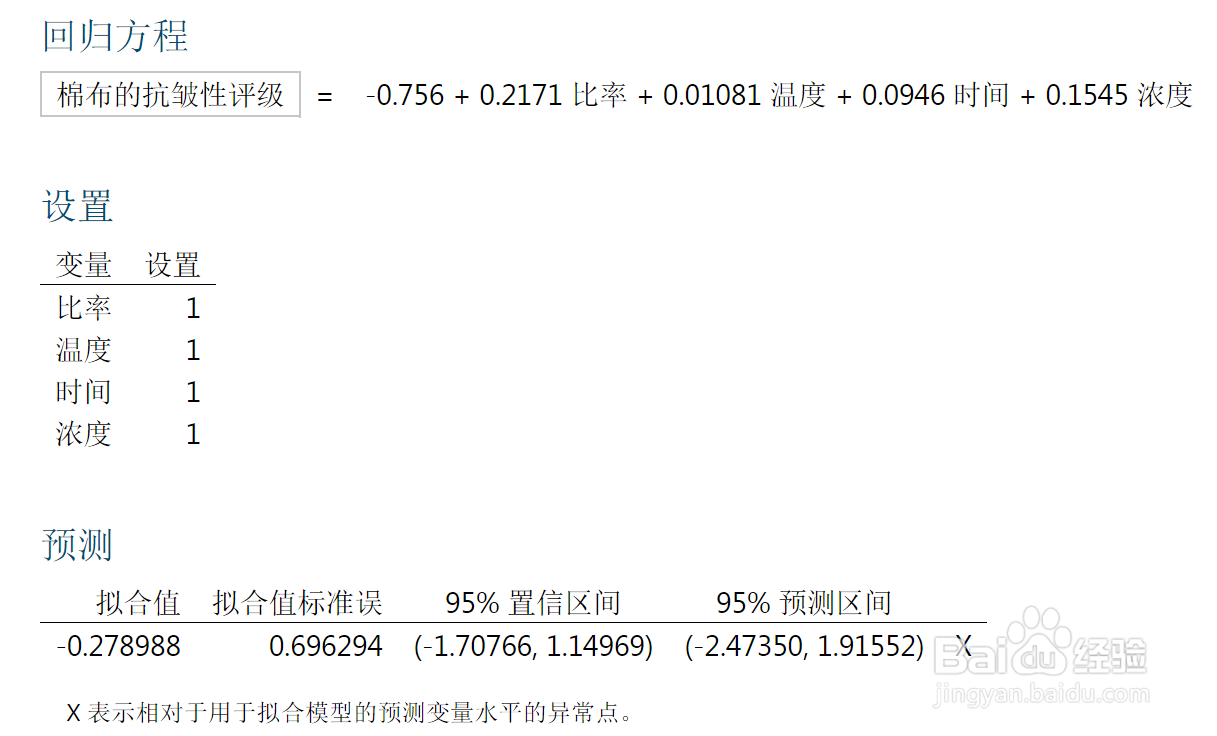
1、确定变量:明确定义了预测的具体楫默礤鲼目标,并确定了因变量。例如某化学家想要了解多个预测变量是如何与棉布的抗皱性(因变量)相关联的。因此,该化学家检测了在不同的凝固时间、凝固温度、甲醛浓度和催化剂比率(自变量)下生产的 32 片棉纤维素。对每片棉布都记录了耐久压烫评级,即抗皱性的度量。
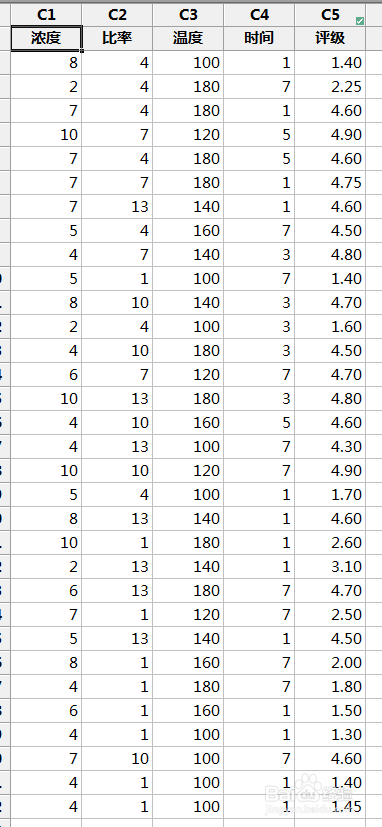
2、建立预测模型:依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析方程,即回归分析预测模型。
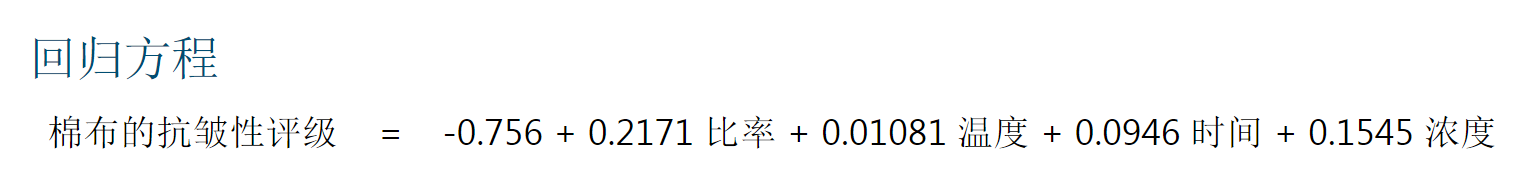
3、进行相关分析:回归分析是因果因素(自变量)和预测因子(因变量)的数学统计分析。 只有当自变量和因变量之间存在某种关系时,建立的回归菱诎逭幂方程才有意义。因此,作为自变量的因子是否与作为因变量的预测对象相关,程度的相关程度以及判断相关程度的程度是在回归分析中必须解决的问题。 相关分析通常需要相关性,并且相关度系数用于判断自变量和因变量之间的相关程度。P<0.05的自变量,相关性显著。
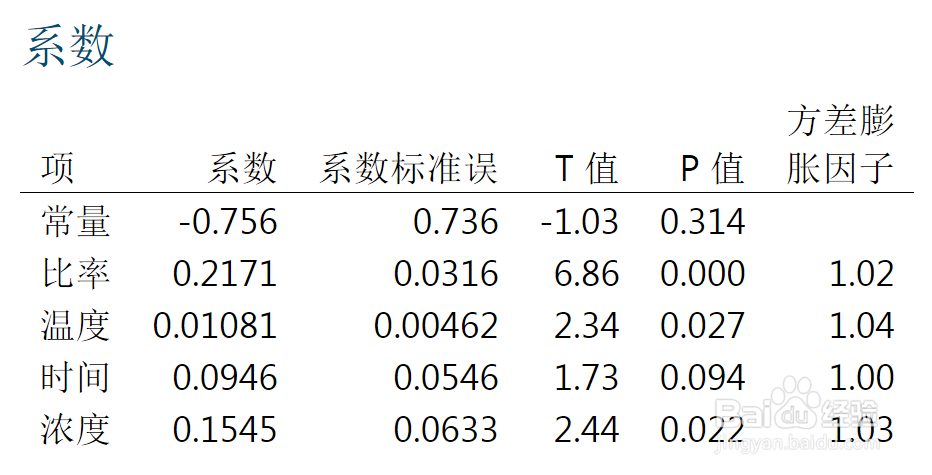
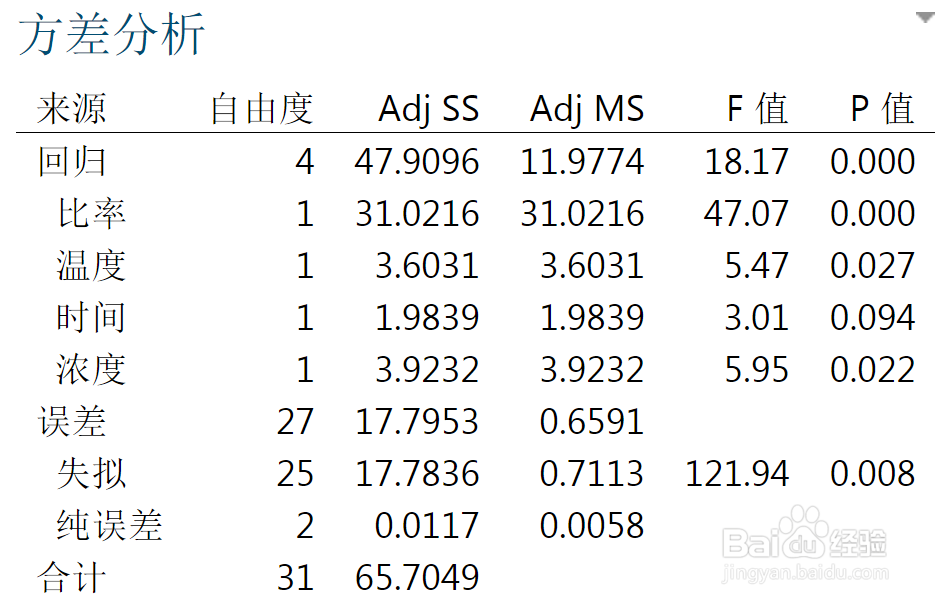
4、计算预测误差:回归预测模型是否可用于实际预测取决于回归预测模型的测试和预测误差的计算。回归方程只能通过回归方程作为预测模型来预测,只有当它通过各种测试且预测误差很小时才能预测。该回归预测模型可以解释因变量73%的响应,是否可用视要求而定。

5、确定预测值:利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。