1、我们要先用我的上一个差分示例,先进行差分分析。具体如下:特别提醒,因为我们这里做的是食品的差分分析,因此以下差分示例要改成食品进行。
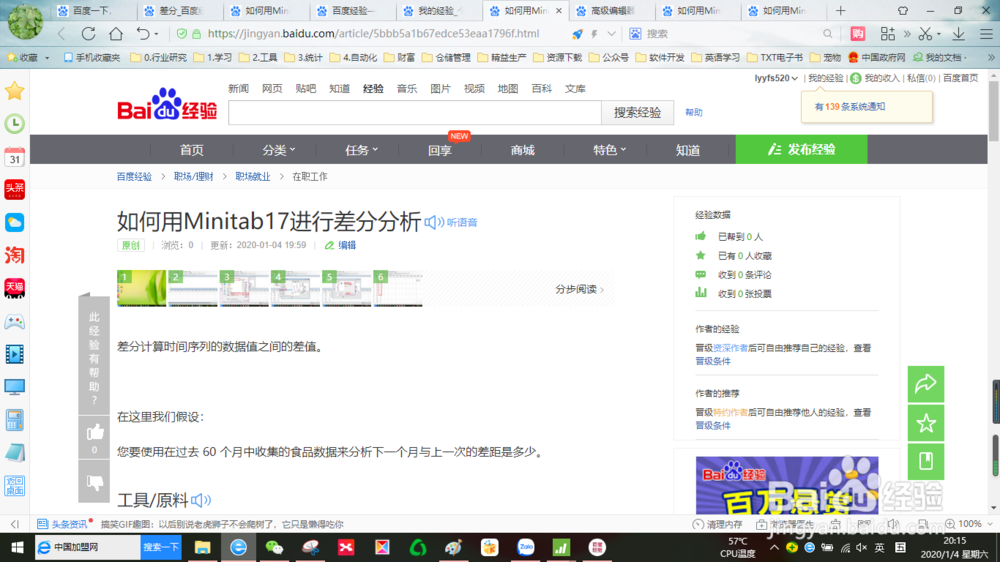
2、左键单击菜单栏选择统计 ---> 时间序列 ---> 滞后。
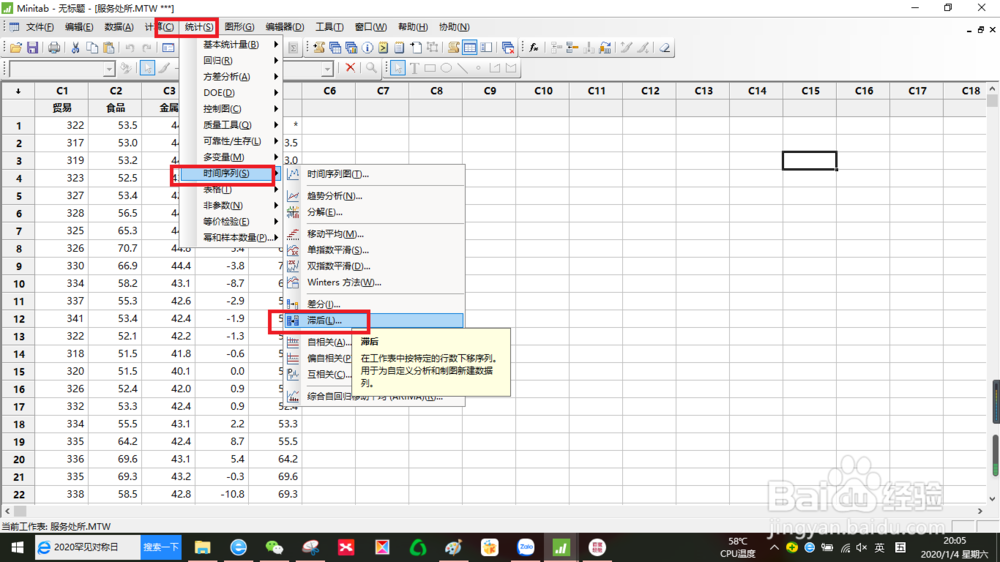
3、在序列中,输入包含要滞后的序列的列服务, 在将滞后存储在中,输入存储列的名称C5,在滞后中输入12然后单击确定。

4、左键单击菜单栏选择 统计 ---> 时间序列 ---> 自相关。

5、序列中,输入食品。单击确定。
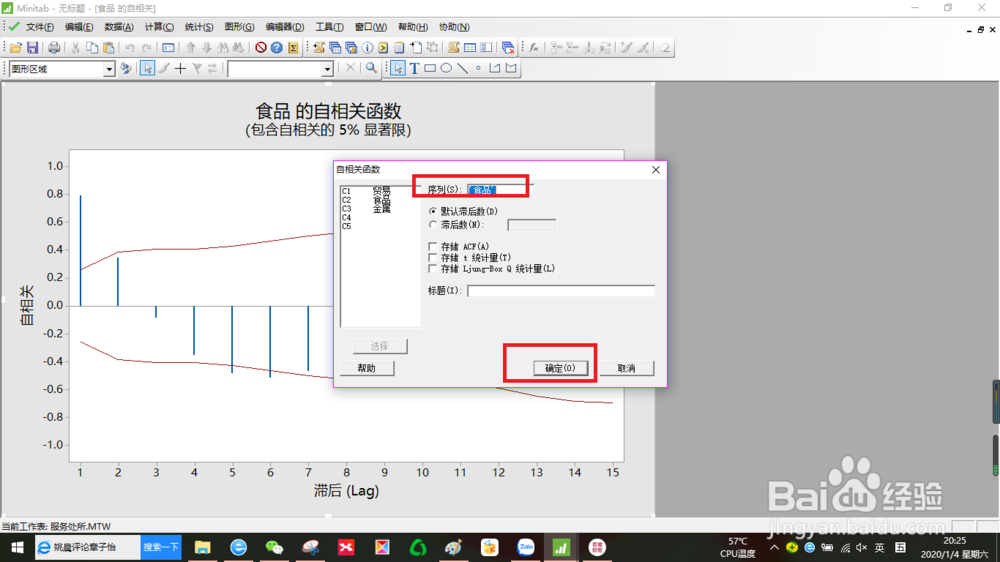
6、我们得出以下结果:
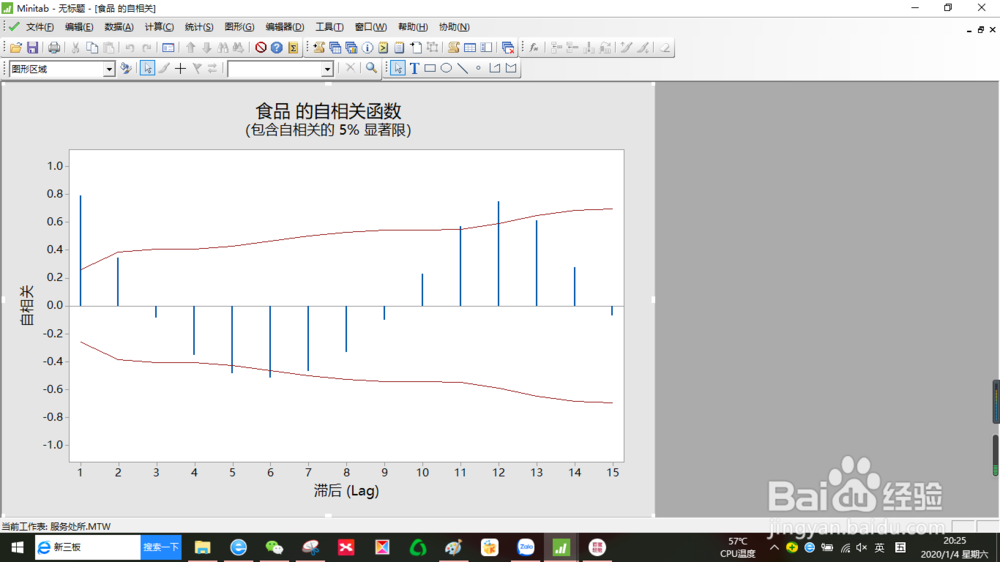
7、解释结果:在会话窗口中,Minitab 饺咛百柘显示自相关、关联 t 统计量和 Ljung-Box Q 统计量 。由于未指定滞后长度,因此自相关对观测值数小于或等于 240 的序列使用默认长度 n/4。Minitab 生成自相关函数 (ACF),其中大约有 a = 0.05 临界带对应于“相关等于零”这一假设。这些数据的 ACF 显示在滞后 1 和 2 处有较大的正峰值,且后续正相关消失得并不快。此模式在自回归过程中很典型。要检验“所有滞后(直到滞后 6)的自相关为零”这一原假设,