1、线段AB始终等于6,这个条件很容易让我们联想到“椭圆规”和“星形线”。点O向右平移6个单位,得到垓矗梅吒x点;点O向上平移6个单位,得到y点;选择O、x、y三点,构造以O为圆心的圆位于第一象限内的圆弧。

2、D是圆弧上的动点,D到x轴的投影是A,D到y轴的投影是B。那么AB就等于6,因为OADB是矩形。
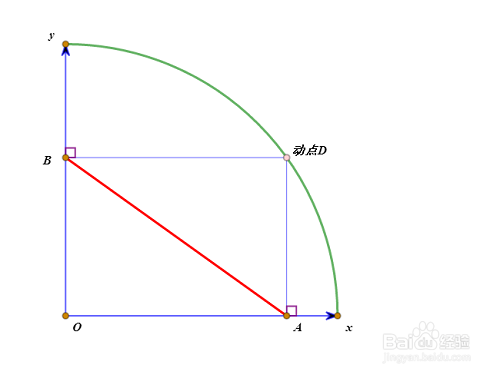
3、过三点ABD的内切圆在第一象限内的半圆弧,C点是这个半圆弧上的动点。由于∠OCD=90°,所以当C、D重合的时候,才有最大值,这个最大值就是OD的长度6.

4、选择D和半圆,构造半癣嗡赧箬圆的轨迹,样本数低一点,定为100就可以了。这样C点的活动区域就是半圆轨迹的覆盖区域。由此可知,C点可以无限接近原点O,但是题意要求C是第一象限内的点,所以O和C不能重合。这样,OC的最小值可以无限接近0,但是却达不到0.

5、线段AB与“椭圆规”的联系在哪里呢?设E点是线段AB内的某个定点,那么根据D来构造E的轨迹,就是椭圆。图中的蓝色曲线,就是椭圆位于第一象限内的那一部分。大家看看,AB什么时候会与这个椭圆相切呢?
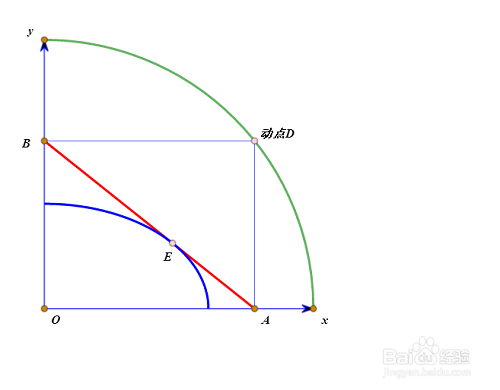
6、线段AB与“星形线”的联系在哪里呢?根据D来构造线段AB的轨迹,就得到AB的包络图形——星形线,下图只画出了第一象限的包络图。

7、拖动E点的同时,跟踪椭圆,可以发现,椭圆的包络线也是刚才的“星形线”,这说明,当E在线段AB内的时候,椭圆始终与星形线相切,且椭圆位于星形线内部。
