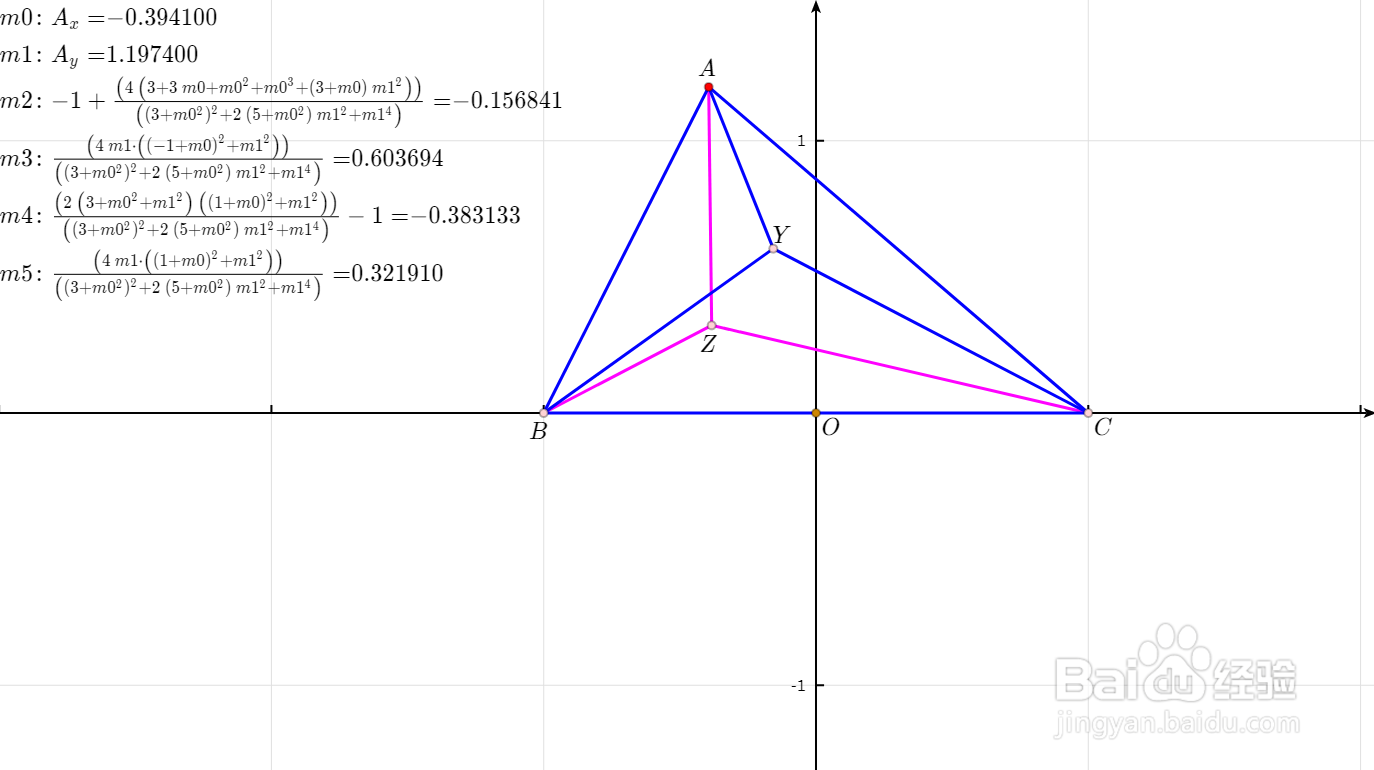
1、打开网络画板的2D作图界面,绘制三角形ABC,其中B的坐标是(-1,0),C的坐标是(1,0),而A是平面上的自由点。
2、测量A的横坐标和纵坐标,分别得到测量数值m0和m1。见图中左上角。

3、计算:m2=-1 + (4 (3 + 3 m0 + m0 ^ 2 + m0 ^ 3 + (3 + m0) m1 ^ 2)) / ((3 + m0 ^ 2) ^ 2 + 2 (5 + m0 ^ 2) m1 ^ 2 + m1 ^ 4)m3=(4 m1 * ((-1 + m0) ^ 2 + m1 ^ 2)) / ((3 + m0 ^ 2) ^ 2 + 2 (5 + m0 ^ 2) m1 ^ 2 + m1 ^ 4)构造直角坐标点Y=(m2,m3)。
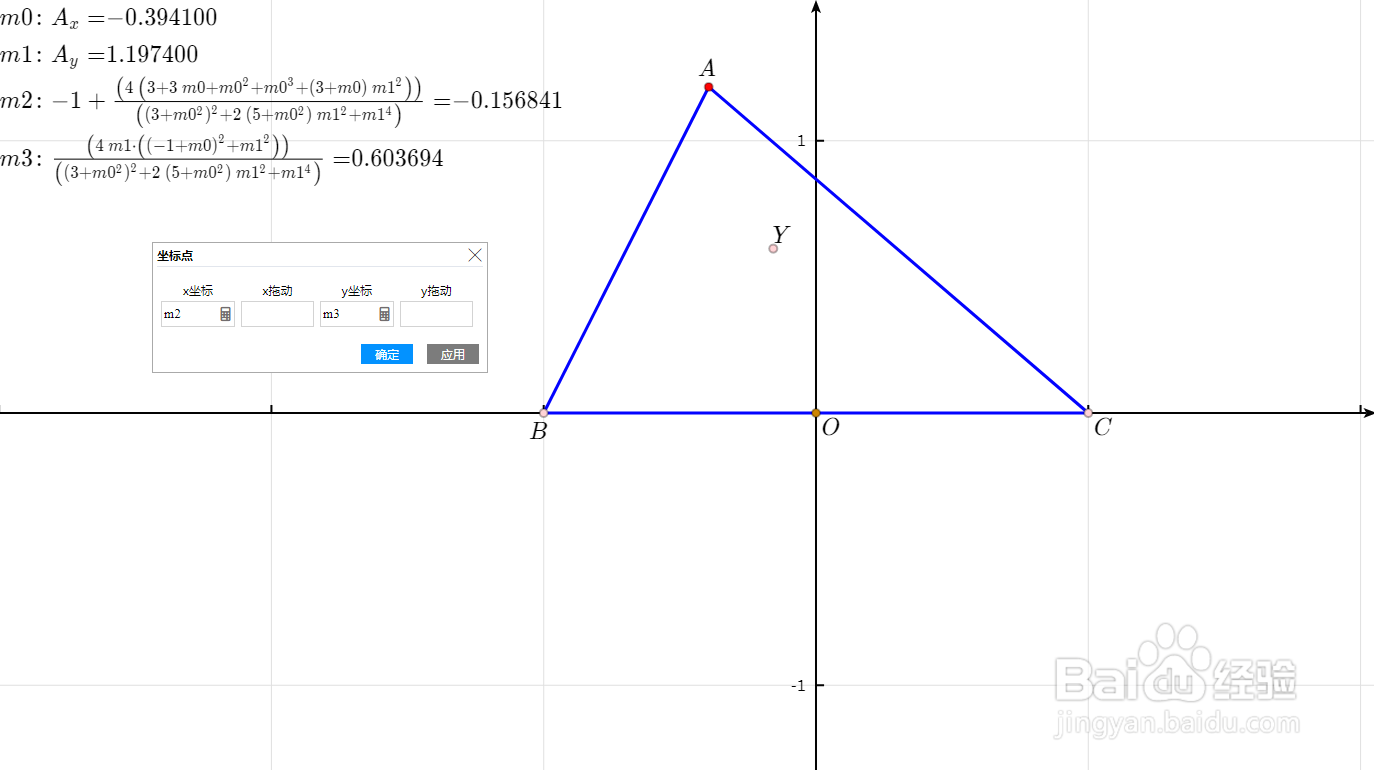
4、这样,Y就是三角形ABC的一个布洛卡点,满足:角YAC=角YBA=角YCB。
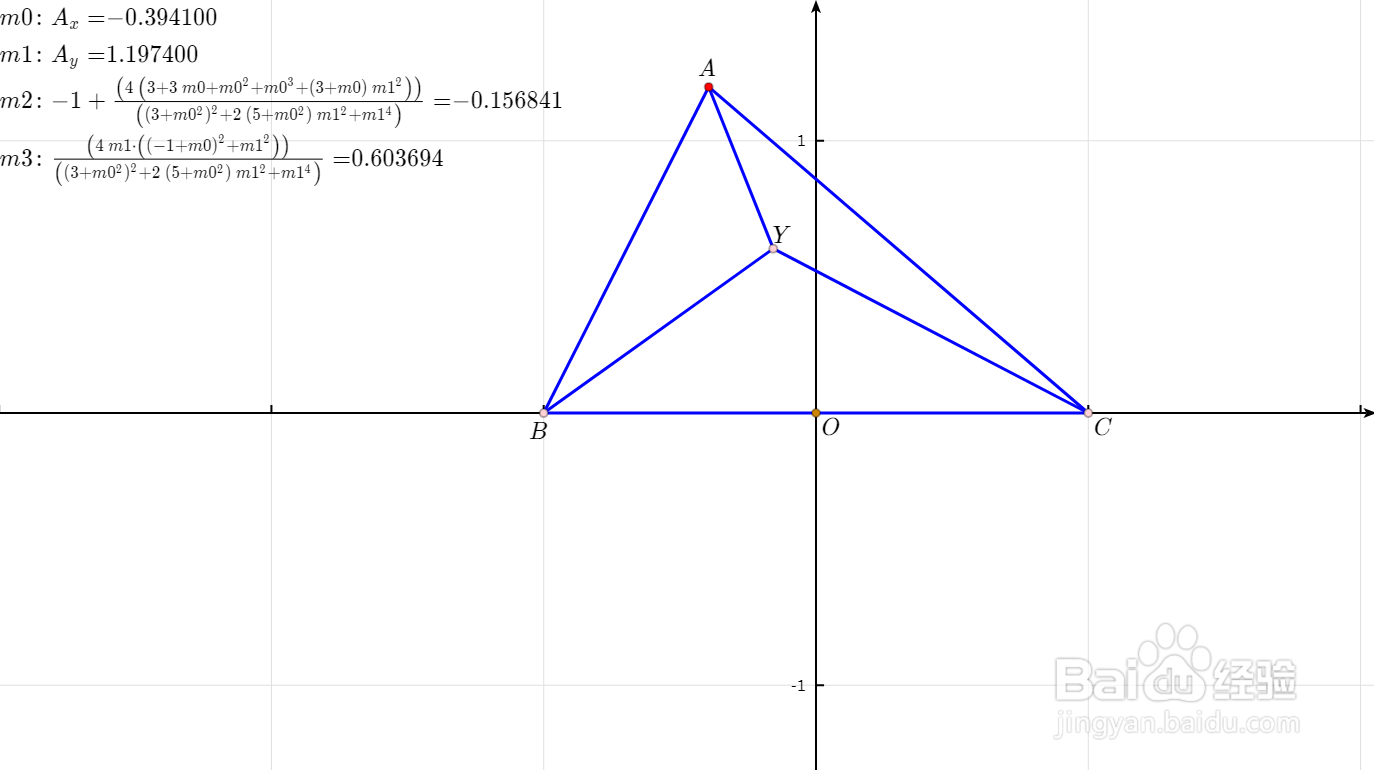
5、计算:m4=(2 (3 + m0 ^ 2 + m1 ^ 2) ((1 + m0) ^ 2 + m1 ^ 2)) / ((3 + m0 ^ 2) ^ 2 + 2 (5 + m0 ^ 2) m1 ^ 2 + m1 ^ 4) - 1m5=(4 m1 * ((1 + m0) ^ 2 + m1 ^ 2)) / ((3 + m0 ^ 2) ^ 2 + 2 (5 + m0 ^ 2) m1 ^ 2 + m1 ^ 4)构造直角坐标点Z=(m4,m5)。

6、Z就是三角形ABC的另一个布洛卡点,满足:角ZAB=角ZBC=角ZCA。
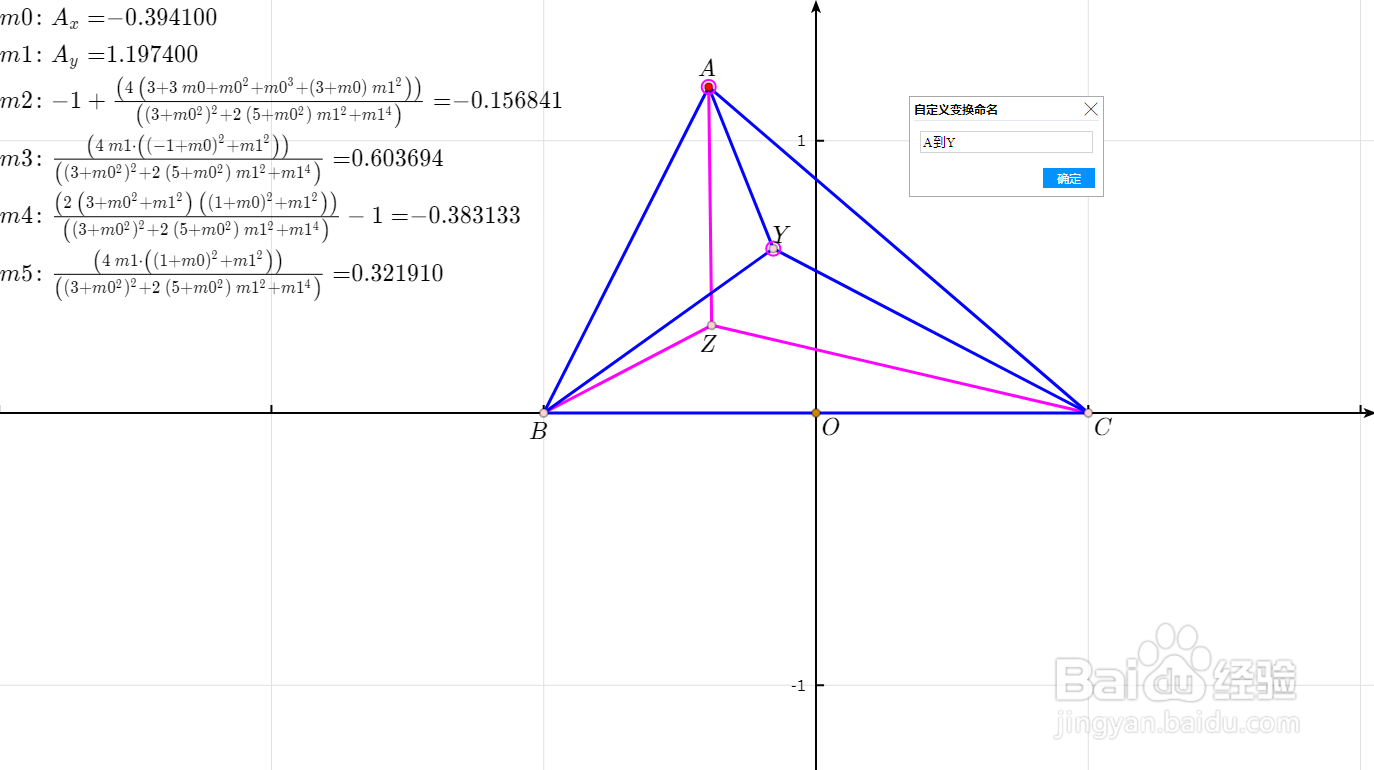
7、用坐标构造布洛卡点的好处在于,当三角形ABC退化为三点共线的时候,布洛卡点不会消失,而是以极限的形式存在着,这样构造的轨迹就可以是连续曲线。回到课件制作:选中A和Y,创建【自定义变换】,命名为【A到Y】;选中A和Z,创建【自定义变换】,命名为【A到Z】。
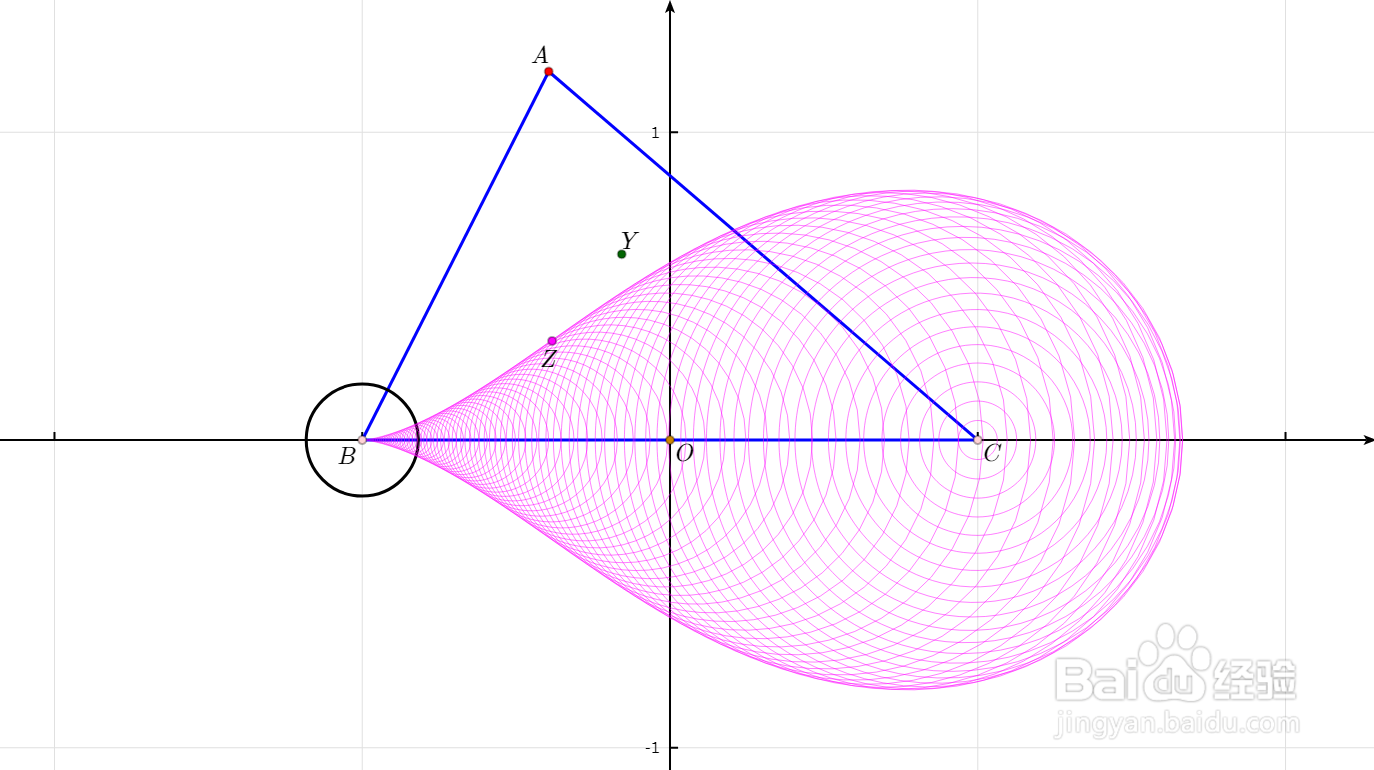
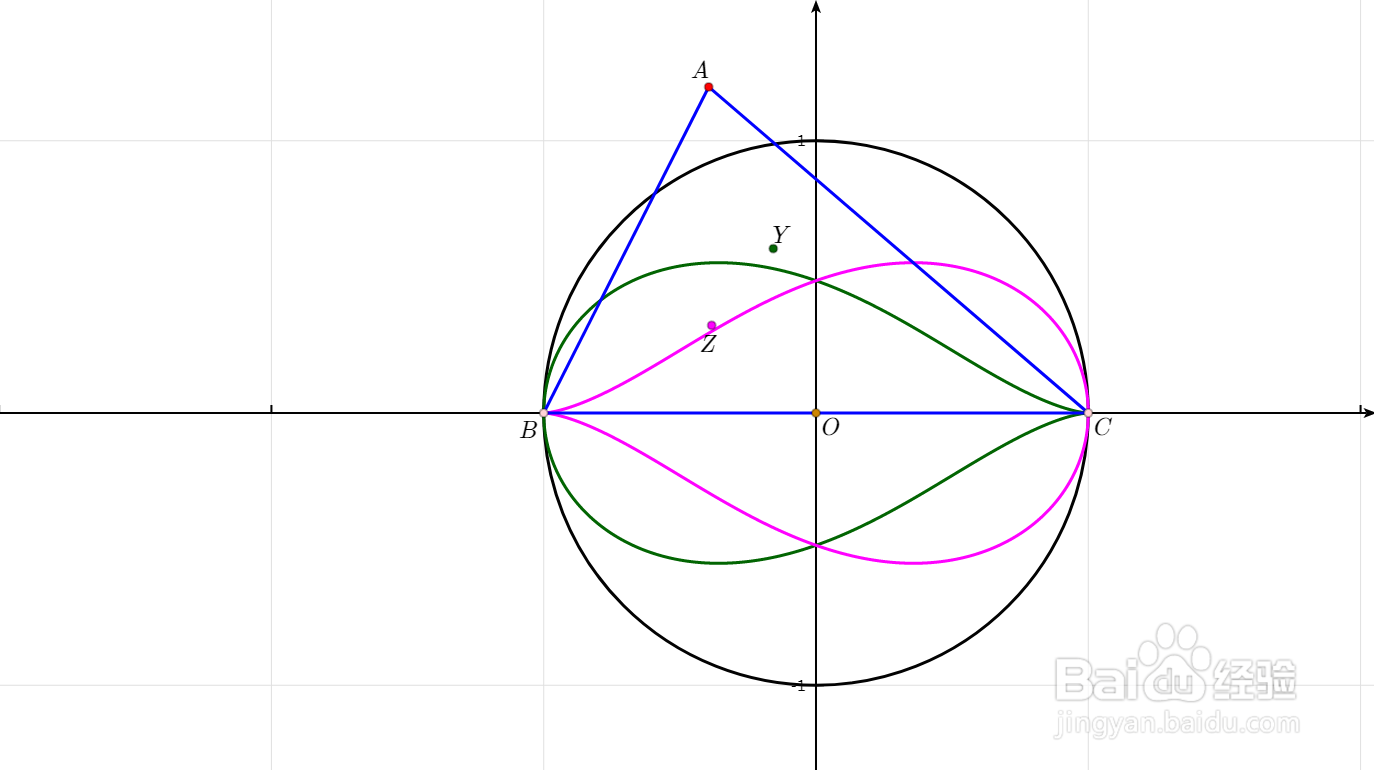
8、构造以BC为直径的圆,图中的黑色曲线;黑色圆经过【A到Y】的变换,得到图中绿色直线;黑色圆经过【A到Z】的变换,得到图中紫色直线。我认为这样的两条曲线都是【水滴形曲线】。
9、以B为圆心、BC为半径的圆:经过【A到Y】的变换,是一条水滴形曲线,图中绿色曲线;经过【A到Z】的变换,是一个圆,图中紫色圆。
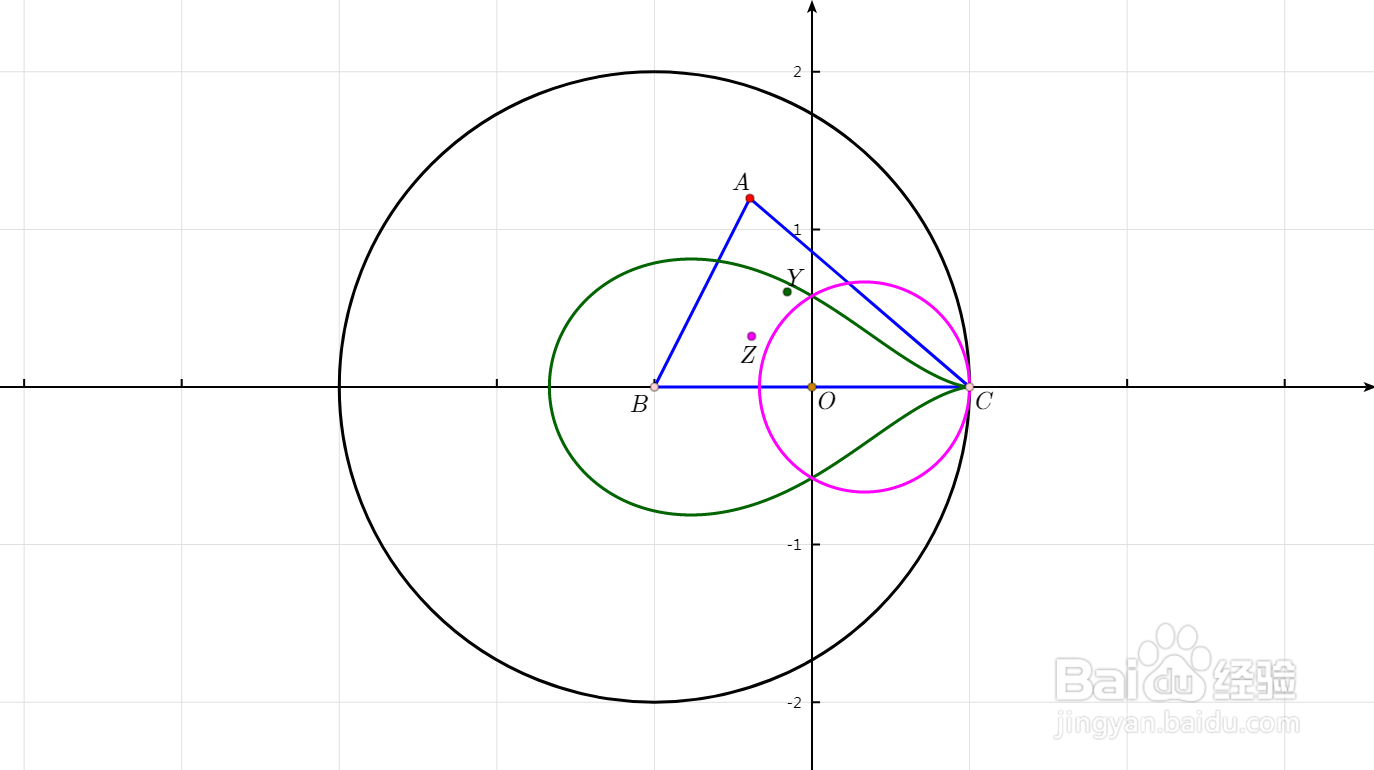
10、实际上,以B为圆心的任意圆,经过【A到Z】的变换,对应的像都是圆。